Pokud se omezíme na jednoduchou stejnosměrnou analýzu, lze dojít k velmi jednoduchému řešení jen na základě závislosti proudu a napětí. Postup je přitom použitelný pro libovolnou nelineární součástku, stačí znát vztah mezi proudem a napětím. U žárovky je závislost proudu mocninnou funkcí napětí. Pokud vám stačí model bez jeho odvození, můžete přejít rovnou na konec článku.
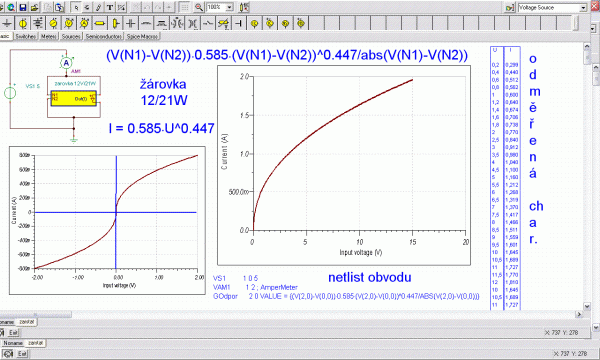
Obr. 1: Odvození voltampérové charakteristiky žárovky
Je také možné odměřenou tabulku VA hodnot vložit do tabulkového procesoru (GRAPH nebo EXCEL) a po vykreslení grafu zvolit mocninnou spojnici trendu se zobrazením regresní rovnice. A protože SPICE algoritmy připouštějí i vložení polynomu, lze z odměřené VA charakteristiky získat model jakékoliv součástky s prakticky libovolnou charakteristikou, pokud na ní nebudou příliš velké zlomy. Free program GRAPH vyžadoval pro výpočet rovnice z tabulky minimálně tři body a z tabulky [1] bylo zadáno: 1,2 V 0,64 A, 6 V 1,268 A a 12 V 1,81 A s výsledkem: I = 0,585U^0,447. Pokud se zpracuje celá zredukovaná tabulka (na obr. 2 vpravo), tak vyjde naprosto shodná rovnice. Zápis funkce lze ještě zjednodušit pomocí funkce znaménka (Sgn) místo funkce absolutní hodnoty (Abs).
Obr. 2: Simulace VA charakteristiky žárovky programem Tina-TI 9
SPICE algoritmy nemají jednoduše říditelný pasivní prvek. Obchází se to pomocí napětím řízeného zdroje proudu G. Poslední verze free programu Tina-TI má v nabídce zdrojů jako poslední volbu průvodce pro návrh složitějšího zdroje. V průvodci byly zvoleny dva napěťové vstupy a jeden diferenciální proudový výstup s tím, že se vstupy a výstupy propojí podle obr. 2 (do pole závislosti je při tvorbě bloku nutné něco zapsat).
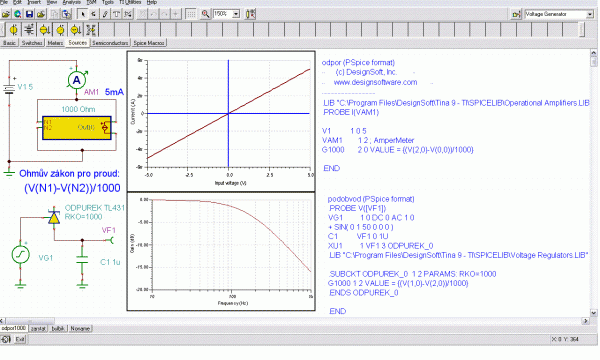
Princip lze nejsnadněji vysvětlit na obyčejném lineárním odporu. Proud obvodem je dán Ohmovým zákonem, přičemž napětí na součástce se určuje jako rozdíl potenciálů – uzlových napětí obvodu. Pro odpor např. 1 kOhm by tedy bylo I = (V(N1) – V(N2))/1000. I přes tuto krkolomnou konstrukci se to při simulaci chová zcela regulérně jako normální odpor. Odpor lze pak ovládat dalšími vstupy anebo použít matematický aparát SPICE (dostupné funkce jsou popsané v nápovědě k programu. Schéma lze i vyexportovat ve formě klasického SPICE netlistu.
Obr. 3: Tvorba podobvodu (subcircuit) odporu
Kdyby se měla součástka (část zapojení) v zapojení vyskytnout častěji, je vhodné ji vytvořit formou makra X. I bez hlubší znalosti SPICE to lze zrealizovat snadno. Horní část zapojení pro stejnosměrnou analýzu (DC transfer characteristic) odporu byla exportována jako PSPICE netlist. V libovolném textovém editoru to pak lze upravit, například vypuštěním přebytečných komentářů. Podrobný postup tvorby podobvodu z netlistu je k dispozici v dokumentaci k programu. Pro jednoduchost byl ale jen přepsán hotový model stabilizátoru volbou ENTER MACRO a CTRLA CTRLV a uložením.
Výhodou makra je snadná modifikace součástky změnou parametrů (zde odporu). Makro má styčné uzly, což lze přirovnat k vývodům integrovaného obvodu s paticí v plošném spoji. Je možné si i nakreslit vlastní značku, ale žárovka se třemi vývody je zcela vyhovující. Přebytečná „anténka“ by mohla sloužit buď jako vstup pro zadání teploty okolí anebo naopak jako výstup, indikující teplotu vlákna. Model žárovky s teplotní sondou vlákna, včetně zajímavé malůvky, je řešen v [2]. To, že se model odporu, tvořený napětím řízeným zdrojem proudu, chová zcela standardně, je ilustrováno střídavou simulací (AC transfer characteristic) integračního článku ve spodní části obr. 3. Tina-TI sice nemá multimediální mód, ale volbou DC analysis nodal voltages lze u zapojených přístrojů alespoň zobrazit měřené hodnoty (5 mA).
Pokud se to shrne, bylo by vhodné mít žárovku jako podobvod a logicky uvádět jako parametry jen to, co je na žárovce napsané (napětí a watáž). Pokud připustíme určitou nepřesnost modelu a podíváme se do tabulek pro různé žárovky [1], zjistíme, že při desetině jmenovitého napětí neklesá výkon kvadraticky stokrát, ale kvůli změně odporu jen 27 až 35 krát. Ve shodě s posledním řádkem obr. 1 zvolíme průměr n = 30 a získáme tím i bez měření chybějící bod A charakteristiky. Po dosazení a úpravě vyjde mocnitel k jako logaritmus desetiny násobku poklesu výkonu k = log3 a vodivost se určí opět dosazením g = P/U^(k+1). Takže místo proložené změřené závislosti I = 0,585U^0,447 získáme odhadnutou závislost, určenou jen nápisem na baňce 12 V/21 W: I = 0,535U^0,477.
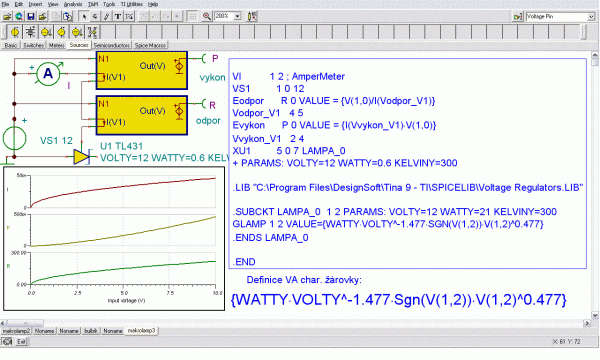
Obr. 4: Výsledný makromodel žárovky pro DC analýzu
Kdyby se měla simulovat i teplota vlákna, tak je to opět snadno řešitelné. Ze vztahu pro teplotní závislost odporu vodiče [1] by se vyjádřila teplota na odporu. A mocninná závislost odporu je odvozena na obr. 1. Jeden bod by se zvolil, např. typických 2 600 stupňů při jmenovitém napětí.
Řízené zdroje lze použít i pro výpočet složitějších závislostí. V posledním zapojení řízené zdroje počítají závislost výkonu a odporu na napětí. Případnou volbou konstanty je možné též měnit měřítka a mít pak závislosti i v jednom grafu. Takto řešený model nelineární součástky je sice velmi jednoduchý, protože je tvořen jediným G zdrojem, ale bohužel nerespektuje zásadní vlastnost žárovky, kterou je tepelná setrvačnost. Ta je podle [3] opravdu značná a vychází zhruba 100 ms. Takže pro TRANSIENT analýzu se jednoduchý model nehodí, protože na rozdíl od polovodičů rožhavené vlákno svítí setrvačností i když jím proud neprochází a samozřejmě i odpor odpovídá teplotě vlákna a ne okamžité hodnotě napětí.
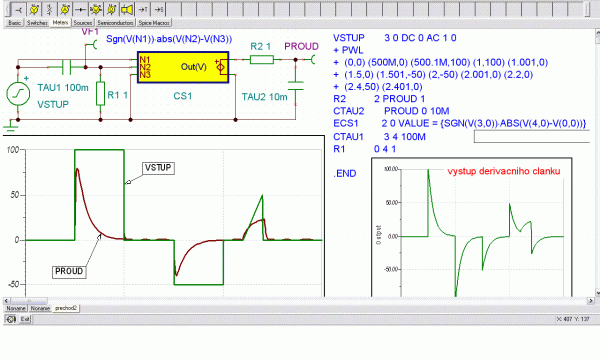
Obr. 5: Přechodová složka proudu při spínání zdroje
Podle [3] po zapnutí žárovky vznikne tepelná, proudová derivační špička. Tuto přechodovou složku by šlo přičíst k původní složce proudu z mocninné závislosti. Problém je ten, že derivační impuls vzniká nejen při zapnutí, ale i při vypnutí, ale žárovkou – na rozdíl od RC obvodu – proud po ukončení obdélníku protékat nebude. Zápornou část by sice šlo zkratovat diodou, ale ne pro obě polarity napětí. K vytvoření žádaného tvaru proudu byly proto usměrněny derivační pulzy pomocí funkce ABS. Správnou polaritu a vynechání špatných špiček zajistí funkce znaménka SGN, která nabývá podle polarity tří hodnot (-1, 0 a +1). Pokud je žádoucí „zaoblit“ i náběžnou hranu, je to možné zajistit integračním článkem s podstatně kratší časovou konstantou.
Na pilové špičce je vidět první nedokonalost modelu, ale tu by šlo odstranit vynecháním RC části. Podstatně horší je, že model nefunguje obecně a špatně by vyhodnotil například nevypnutí až na nulu. Tudy tedy cesta obecně nevede. Ale každopádně tento testovací zdroj PWL dobře prověří případný model. Zápis průběhu PWL zdroje je tvořen posloupností souřadnic bodů času a napětí.
Obr. 6: Žárovečka, poskládaná ze sklenice od dětské výživy a s tuhou od pentelky, coby vláknem
Obr. 7: Po „vakuování zapálenou svíčkou“ bylo dosaženo celé jedné minuty svitu
Závěr:
Nelineární závislost proudu na napětí na žárovce v ustáleném stavu lze vyjádřit mocninnou závislostí I = gU^k , kde k = log (n/10) a n je kolikrát klesne výkon při desetině jmenovitého napětí (typicky 30 krát a k = 0,477). Vodivost g = Pjm / Ujm^(1+k), takže pro žárovku bude po dosazení I = (Pjm*Ujm^-1,477)*U^0,477. Zadáním jmenovitého výkonu a napětí žárovky získáme rovnici nelineární charakteristiky, procházející jmenovitým pracovním bodem žárovky. Tuto rovnici lze snadno zadat jako value do definice napětím řízeného zdroje proudu G.
Postup je aplikovatelný na libovolný nelineární prvek s odměřenou charakteristikou, protože SPICE připouští i použití polynomu a ty lze vygenerovat v tabulkovém procesoru (GRAPH nebo EXCEL) jako spojnici trendu.
Download a odkazy:
[1] http://kdf.mff.cuni.cz/tabor/2006/projekty/zarovka.pdf
[2] http://www.intusoft.com/nlpdf/nl11.pdf
- GRAPH: http://www.padowan.dk/download/
- TinaTI: http://www.ti.com/tool/tina-ti