Biologové jim sdělili, že by dokázali s pomocí genetiky vytvořit neporazitelného koně, ale trvalo by to 200 let a stálo 100 miliard dolarů. Statistici uvedli, že by dokázali předpovědět výsledek každého dostihu, ovšem s náklady 100 milionů dolarů na dostih a úspěšností deset procent. Nakonec si vzali slovo fyzici a prohlásili, že také mohou předpovědět výsledek každého dostihu, a jejich metoda je jednoduchá a levná. Investoři napjatě poslouchali. „Začali jsme s několika zjednodušujícími kroky. Prvním je předpoklad, že každý kůň je dokonalá koule...“ (Ewan Birney, náměstek ředitele Evropského ústavu bioinformatiky EBI)
Model žárovky, který vychází ze změřených voltampérových charakteristik tepelných koulí, je sice statický přesný, ale v dynamických režimech „pokulhává“. Pokud se voltampérové charakteristiky znormují, mají VA charakteristiky žárovek vzhledem ke stu procentům jmenovitých hodnot stejný tvar. Takže větším problémem je dynamický model. Podle [1] je časová konstanta tepelného děje vlákna v desítkách milisekund. Pro začátek zvolíme stovku a nakonec, pro minižárovku v generátoru, pětinu (20 ms). Ohřev a chladnutí materiálu má exponenciální průběh podobně jako nabíjení a vybíjení kondenzátoru. Dokonce se ve stavebnictví definují tepelné odpory, kapacity, toky. Teplotní průběh a tedy i odpor vlákna žárovky je tedy možné simulovat velmi jednoduše integračním článkem. Ohmův zákon pro zdroj proudu řízený napětím I = U/R přináší díky operaci dělení nečekané problémy a to i přesto, že dělení nulou je SPICE vyhodnoceno nikoliv jako chyba, ale jako limita (velmi velké číslo). Vhodnější je proto použít pro simulaci Ohmova zákona tvar U = RI a tedy proudem řízený zdroj napětí.
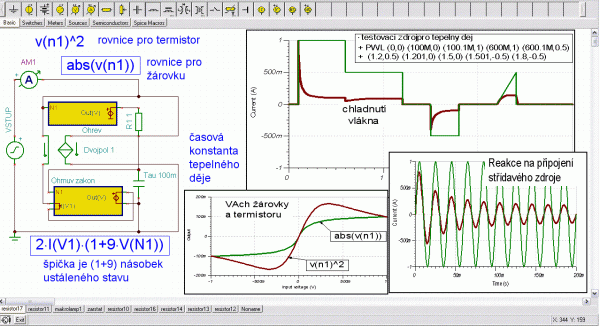
Obr. 1: Dynamický model žárovky s proudem řízeným zdrojem napětí E
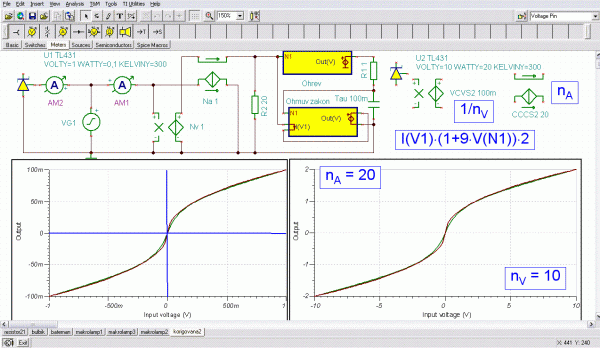
Protože potřebujeme žárovku jako dvojpól, byl mezi žluté bloky vsunut ještě proudem řízený zdroj proudu, abychom meřený proud podle Ohmova zákona dostali ven z obvodu. Jako vstupní hodnota ohřevu by mělo být teplo (mocnina). Ukázalo se však, že výsledná charakteristika by pak měla tvar charakteristiky termistoru a do této části charakteristiky se už vlákno nedostane, protože se dřív spálí. Místo toho proto byla pro nabíjení tepelného kondenzátoru zvolena absolutní hodnota vstupního napětí. Volbou násobku napětí snímaného na kondenzátoru v rovnici je definován pokles vzhledem k maximu po odeznění tepelného děje. Byla zvolena jedna desetina špičky (v obrázku z 1 A na 100 mA). Model reaguje správně na lomený lineární zdroj PWL, na připojení do obvodu střídavého napětí a má i správný tvar voltampérové charakteristiky a přitom lze snadno modifikovat setrvačnost i špičku vzhledem k ustálenému stavu.
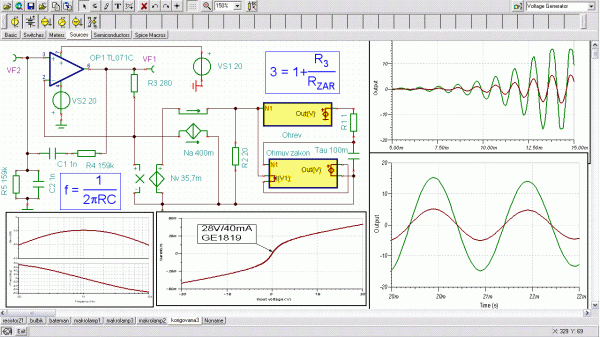
Obr. 2: Frekvenční závislost vlákna a snímání teploty wolframu
Protože máme žárovku jako odpor, můžeme přidáním indukčnosti vlákna vytvořit dolní propust a rozšířit případně simulaci o chování žárovky při vysokých kmitočtech. I tohle má smysl, protože v jednoduchém měření vlnových délek se pro indikaci maxim stojatých vln vybuzených na Lecherově vedení používal žárovkový dipól. Stejně snadno lze z modelu „vytáhnout“ informaci o teplotě vlákna, protože je závislá na odporu vlákna. Stačí ve shodě s literaturou odhadnout rozžhavený wolfram na 2 600 stupňů a případně k tomu přičíst pokojovou teplotu, aby vlákno bez proudu nemrzlo. Absolutní hodnoty teploty sice důležité nejsou, ale tvar průběhu ano, protože může indikovat složitý přechodový děj při ustalování amplitudy kmitů po náběhu po zapnutí Wienova generátoru (obr. 7). Anebo možná by bylo vhodnější místo teploty indikovat přímo odpor vlákna pro urychlení návrhu záporné zpětné vazby.
Obr. 3: Doladění tvaru charakteristiky srovnáním podle přesnějšího modelu
Po vyřešení dynamického chování je zapotřebí doladit tvar VA charakteristiky. K tomu byl použit model z
předchozího článku, který vycházel ze skutečných změřených charakteristik (např. pro 12 V/21 W: I = 0,535U^0,477 a mimochodem blíží se to odmocnině z napětí, takže by to šlo ještě zjednodušit). Srovnáním charakteristiky bylo zjištěno, že je zapotřebí charakteristiku z dynamického modelu „zešikmit“ (zvětšit vodivost). Zde se ukazuje výhoda metody, která umožňuje kombinovat rovnice ve žlutých blocích zdrojů se skutečným zapojením. Kýženého výsledku bylo dosaženo paralelním připojením odporu 20 Ω. Blok zdroje lze případně použít i pro výpočet relativní chyby charakteristiky v procentech. Shoda je téměř dokonalá, samozřejmě s výjimkou příliš zlinearizovaného počátku, což bylo pro jistotu ověřeno pro dvě různé žárovky a tím byla potvrzena hypotéza o možnosti použít jeden normalizovaný tvar voltampérové charakteristiky tepelné koule.
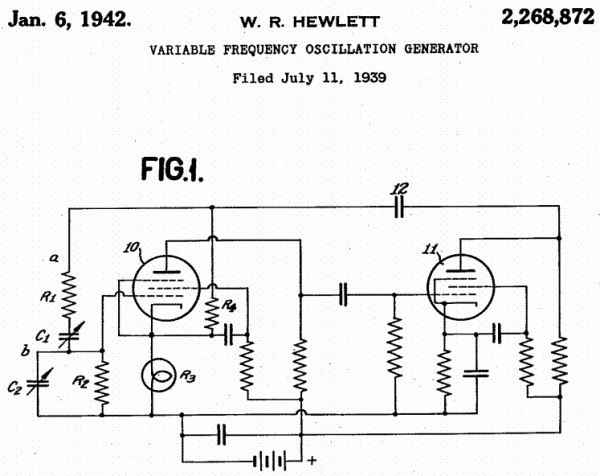
Obr. 4: Žárovka R3, použitá ke stabilizaci amplitudy kmitů
W. Hewlett zkonstruoval Wien bridge oscillator v roce 1939 a po válce spolu s D. Packardem začali s výrobou RC generátoru HP200A. Takže toto zapojení se žárovkou stálo u zrodu firmy Hewlett-Packard Company. Zapojení je dokonalé. Pásmová propust v kladné zpětné vazbě, která je tvořená Wienovým článkem, vybere kmitočet generátoru. A v záporné vazbě nelinearita a tepelná setrvačnost žárovky stabilizuje amplitudu podobně jako James Wattův odstředivý regulátor stabilizuje otáčky parního stroje. Prubířským kamenem správnosti SPICE modelu bude tedy stabilizace kmitů RC generátoru.
Obr. 5: Rozkmitání generátoru po zapnutí zdroje
Dole na obrázku jsou odsimulovány frekvenční a fázové charakteristiky pásmové propusti naladěné na 1 kHz a VA charakteristika žárovky GGE 1819. Propust má při kvazirezonančním kmitočtu přenos 1/3 bez fázového posuvu, takže zpětnou vazbou je zapotřebí nastavit zesílení na 3, aby byla splněna oscilační podmínka. Vtip je v tom, že po zapnutí je vlákno studené a zesíleni je větší než tři. V zesilovači jsou odpory, které tepelně širokopásmově šumí. Kladná zpětná vazba zesílení zesilovače naopak zvyšuje a protože je selektivní, vybere ze šumu jen naladěný kmitočet a obvod se na tomto kmitočtu rozkmitá. Záporná vazba pak zajistí rovnováhu a ustálení stavu, protože po rozkmitání se vlákno žárovky ohřeje, jeho odpor vzroste a zesílení klesne. Jako inspirace konkretního zapojení byly zvoleny stránky [2], protože na nich byly pěkné fotky a konkrétní žárovka. Po zvětšení zpětnovazebního odporu se obvod docela ochotně rozkmital z nuly (v analýze TRANSIENT je zapotřebí nastavit nulové počáteční podmínky). Při kontrole kmitočtu na detailu průběhu vpravo dole se ale ukázalo, že amplituda klesá a po nakmitání generátoru obvod oscilace neudrží. Pomohlo další zvětšení odporu zpětné vazby a snížení teplotní setrvačnosti minižárovky na reálnějších 20 ms.
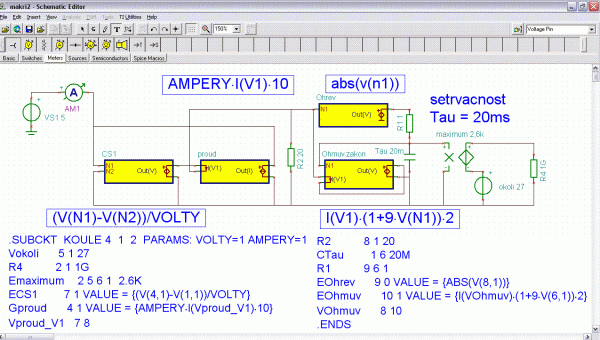
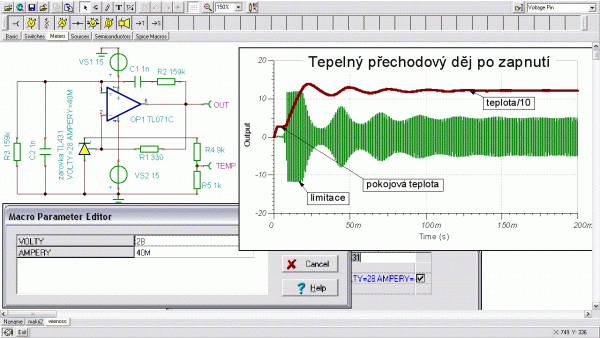
Obr. 6: Tvorba makra (subcircuit) žárovky
Vytvoření podobvodu je náročné na pečlivost a pozornost. Je vhodné si pomoci nějakou součástkou zapojenou mezi zem, která se pak smaže, což usnadní číslování uzlů, protože jinak by model žárovky mohl být zapojován pouze na zem (na obr. 6 zůstala chyba: v EOhrev 9 0 má být 9 1). Je to třeba ohlídat, protože finta s pomocným odporem se v rovnicích nepromítla. Se značením země si nejsem jistý, zda značení nultého uzlu má opravdu globální platnost. Problémem bylo i předavání parametrů (jmenovité napětí VOLTY a proud AMPERY), protože se mi to nedařilo „vnutit“ jako parametr nějakého zdroje. Nakonec se to obešlo jako parametrický člen rovnice řízeného zdroje. Vyvedena byla ven i teplota vlákna, protože může usnadnit pochopení elektrického přechodového děje, způsobeného kolísáním teploty vlákna žárovky.
Obr. 7: Výsledek celé práce – přechodový děj po zapnutí RC generátoru
Generátor se rozkmitá vlastním šumem, naběhne až do limitace, vláknu se přitom zvedá teplota a tím klesá zesílení. Pokles zisku je ale příliš velký, takže amplituda začne klesat a vlákno chladnout. Děj se několikrát zopakuje a až po pár dalších výkyvech nastane rovnováha. Model má opravdu blízko k odstředivému regulátoru otáček po roztočení stroje. SPICE simulace kmitů je choulostivější záležitost a často zapojení nekmitá i když by teoreticky mělo. Někdy pomůže změna typu zesilovače a někdy třeba jen délka časového úseku, ale tady to vyšlo dobře.
Obr. 8: Zapojení součástek do kontaktního pole
Toto zapojení se navíc dá snadno postavit a je to jeden z mála opravdu dokonalých obvodů, jednoduchých, snadno pochopitelných a fungujících. Pro ilustraci dvě fotky z realizace generátoru na kontaktním poli [2].
Obr. 9: Testování zapojení Wienova oscilátoru
A na závěr, pokud by si chtěl někdo hrát se simulacemi, tak model žárovky v TinaTi získáte vložením následujícího netlistu do SPICE modelu regulátoru:
.SUBCKT LANICEK 4 1 2 PARAMS: VOLTY=1 AMPERY=1
Vokoli 5 1 27
R4 2 1 1G
Emaximum 2 5 6 1 2.6K
ECS1 7 1 VALUE = {(V(4,1)-V(1,1))/VOLTY}
Gproud 4 1 VALUE = {AMPERY*I(Vproud_V1)*10}
Vproud_V1 7 8
R2 8 1 20
CTau 1 6 20M
R1 9 6 1
EOhrev 9 1 VALUE = {ABS(V(8,1))}
EOhmuv 10 1 VALUE = {I(VOhmuv)*(1+9*V(6,1))*2}
VOhmuv 8 10
.ENDS
Download a odkazy: