Slovo úvodem...
Ve většině odborných časopisů a magazínů se již vyskytla alespoň zmínka o kvantových počítačích. Jenže skoro žádný článek buď neposkytoval dostatek informací typu „o co tam vlastně opravdu jde“ a nebo v případě hodně odborných článků již prakticky nelze popisované věci pochopit (pokud nejste zdatný matematik a fyzik). Protože mě to však velmi zajímalo, zkusil jsem si postupně nastudovat co nejvíce informací, které jsem byl schopný se svými základními znalostmi kvantové fyziky pochopit a ve výsledku pokusil vytvořit takový článek, který bude odpovídat na většinu otázek běžného elektroinženýra, který o to má zájem, ale zároveň si z toho něco může odnést i běžný člověk. Myslím si, že kvantové počítače jsou tak zásadní systém pro budoucnost, že i běžný technik by měl mít představu, co to vlastně je...
Poznámka: Čtenářům znalým kvantové fyziky se předem omlouvám za nepřesnosti, které mohly vzniknout mými silně limitovanými znalostmi kvantové fyziky a nebo byly vytvořeny záměrně pro účel snazšího přiblížení základních ideí principu funkce kvantových počítačů.
Základní stavební jednotka - Bit vs. Qubit
U všech současných (klasických) počítačů je základní jednotka informace „bit“, jehož stav za všech okolností musí být buď 1 nebo 0. Skupina 8 bitů pak dohromady tvoří bajt (byte), což je známý základ celé reprezentace číslicových dat.
V případě kvantových počítačů pak je základní jednotkou dat tzv. Qubit (kvantový bit). Rozdíl proti běžnému bitu je ten, že nejen může nabývat hodnot 1 a 0, ale současně i libovolné hodnoty mezi tím, tedy stavy „ani 1 ani 0“. Logické stavy qubitu se proto označují symbolem |0> a |1>. Matematicky se dá výsledný stav qubitu interpretovat jako superpozice pravděpodobnosti stavů |0> a |1>, tedy že s určitou pravděpodobností A je stav |1> a s určitou pravděpodobností B je stav |0> (odborně matematicky je qubit popsán jako dvourozměrný Hilbertův prostor kvantových stavů).
Matematický zápis stavu qubitu:
|u> = A |1> + B |0>,
kde |u> je stav qubitu, A a B jsou kompletní čísla pravděpodobností stavů |1> a |0>, pro která platí vztah A2 + B2 = 1.
Celý tento zápis pak lze graficky modelovat povrchem kulové plochy (tzv. Blochova sféra) – viz obrázek vedle.
Samozřejmě stav „ani 1 ani 0“ může platit pouze v případě, že se na něj nedíváme. Protože, když se na něj podíváme „digitálním okem“ musí mít prostě vždy stav buď 0 nebo 1. Prostě nám v tento moment (tzv. Moment měření) se stav qubitu „přehoupne“ (zkolabuje) na jednu stranu, podle toho, jaká je aktuálně pravděpodobnější. Prostě jako pověstný jazýček na vahách, který je blízko středu, ale vždy se prostě převáží na jednu či onu stranu. Protože však kvantové výpočty, kterých se qubit účastní, pracují s těmi neurčitými stavy (pravděpodobnostmi stavů 1 a 0), tak zkolabování stavu každého qubitu prostě nenávratně zničí celý výpočet. Proto u kvantových výpočtů, na rozdíl od běžných výpočtů běžných procesorů (PC), není možné se během „počítání“ kouknout „jak to vypadá“. Z programátorského pohledu nelze provádět ladění (debuging) algoritmu. Prostě jen musíme definovat vstupní hodnoty a po dokončení výpočtu odečíst výsledek.
Tyto všechny vlastnosti vycházejí z principu kvantové fyziky, tedy fyziky, která se uplatňuje při práci na úrovni jednotlivých atomů, elektronů a fotonů. Konkrétně jde o Heisenbergův princip neurčitosti (též Heisenbergovy relace neurčitosti). Máme-li systém v neznámém stavu, nemůžeme jej bez narušení změřit. To znamená, že do systému nelze nijak zasahovat, protože jakékoliv měření průběh výpočtu naruší (každý qubit získá konkrétní stav a superpozice se zruší). Proto při technické realizaci je třeba zabezpečit naprostou izolaci proti působení všech možných vnějších vlivů.
Pokus o jednoduché přiblížení funkce kvantového výpočtu
Dlouho před psaním článku jsem přemýšlel, jak základní ideu principu kvantového počítání popsat tak, aby ji pochopilo co nejvíce čtenářů, včetně těch bez vysokoškolského technického vzdělání.
Představme si dnes všem blízkou situaci nejisté budoucnosti vlivem ekonomické krize v podobě soukromého výrobce „čehokoliv“. Tento drobný živnostník nám reprezentuje kvantový počítač. Pokud takový člověk zůstane ideálně odříznutý od jakýchkoliv informací o aktuální ekonomické situaci v EU, tak na dotaz, zda se mu ekonomicky bude v budoucnu dobře dařit, patrně odpoví „nevím“ (stav informace někde mezi hodnotami ANO = stav. 1 a NE = stav. 0), nebo pokud se jej budeme ptát pravidelně opakovaně s tím, že musí vždy říct jen ANO nebo NE, tak někdy řekne ANO a někdy zase NE, podle aktuální nálady či aktuálním počtu prodaných výrobků (negativní vlivy zvenčí v podobě rušení také negativně ovlivňují funkci kvantového počítače).
Pak tomu živnostníkovi někdo řekne, že se mu v budoucnu bude dařit podle toho, jaký bude ekonomický stav v ČR, který je také závislý na stavu Německa a méně na stavu Polska. To je stav, kdy jsme kvantový počítač „naprogramovali“ algoritmem se 3 vstupy (ekonomický stav v ČR, Německu a Polsku) a jedním výstupem (bude se dařit v budoucnu?). Dokud však nebude živnostník mít informaci o aktuální ekonomické situaci v ČR či alespoň v Německu či Polsku, odpovědi budou pořád stejné, jako předtím.
Pak se ale doslechne, že v Německu je ekonomická situace špatná. To situaci změní a vyhodnotí, že s větší pravděpodobností se mu asi dařit nebude a častěji bude říkat „NE“. A poté, co se dozví, že ekonomická situace je špatná v ČR, v Německu i Polsku a tedy vyhodnotí, že s největší pravděpodobností se mu bude dařit hůře, pak na dotaz reportéra vždy řekne „NE“, tedy že se mu dobře dařit nebude.
A takto velmi zhruba podobně v principu pracuje i kvantový počítač. Je to uzavřená krabička, která současně obsahuje všechny více i méně možné možnosti. Proto pokud se podíváme na výstup, jednou dostaneme stav 1 a podruhé stav 0 – pravděpodobnost, že výstup má být 1 či 0 je stejná. Pokud počítači dodáme na vstup úplná data, a podíváme se na výstup, vždy získáme stejný stav, např. stav 1, protože pravděpodobnost, že má být výstup ve stavu 1 je vysoká a tedy při čtení se vždy hodnota překlopí na stranu 1. Protože však počítač uvnitř ve svých qubitech současně obsahuje všechny možné varianty výpočtu, je výsledek vygenerován velmi rychle.
Klasický vs. Kvantový počítač
 Klasický počítač pracuje tak, že algoritmus řeší jako konečnou sekvenci postupně vykonávaných instrukcí nebo řeší problém stylem krok-za-krokem. I kvantový počítač postupuje stylem krok-za-krokem, ale s tím rozdílem, že každý krok je realizován kvantovým výpočtem.
Klasický počítač pracuje tak, že algoritmus řeší jako konečnou sekvenci postupně vykonávaných instrukcí nebo řeší problém stylem krok-za-krokem. I kvantový počítač postupuje stylem krok-za-krokem, ale s tím rozdílem, že každý krok je realizován kvantovým výpočtem.
Zatímco klasický počítač prostě musí při výpočtu či vyřešení algoritmu čekat na úplné informace na vstupu, aby mohl úlohu vůbec začít řešit, kvantový počítač již má úlohu neustále jakoby „předřešenou“ a tím je výpočet složitých algoritmů mnohonásobně rychlejší než u nejrychlejších klasických počítačů. Na druhou stranu nemůžeme se nikdy podívat dovnitř do průběhu výpočtu, protože v tu chvíli do kvantového počítače dodáme „nadbytečné“ informace do zpracování (z pravděpodobnosti určitého stavu vnitřního registru uděláme jistotu), čímž prakticky zničíme průběh kvantového výpočtu a výsledek je chybný.
To je však jen velmi hrubé přiblížení. Z technického hlediska je lepší přiblížení k paralelnímu zpracování dat. Konečně i náš mozek zpracovává data paralelně a proto přiblížení základní funkce naším mozkem je tak trošku namístě. Kvantový počítač jako by současně počítal všechny více či méně možné varianty algoritmu či řešení problémů a nakonec výsledek s největší pravděpodobností je ten výsledný správný. Proto se kvantové počítání velmi hodí pro situace a algoritmy, kdy hledáme nějaké neznámé řešení, jako například vyhledávání v databázi či hledání faktoriálu čísla. Zatímco běžné algoritmy prostě postupně prochází jednotlivé možnosti řešení „jeden za druhým“ u kvantového počítače toto vyhledávání probíhá jakoby paralelně současně u všech možných variant, což je ve výsledku tak obrovská rychlost výpočtu kvantového počítače.
Výpočet veškerých dlouhých číselných řad je prostě ideální úloha pro kvantový počítač. Ukažme si je na příkladu šachů. Když počítač generuje tah, prochází všechny možné tahy (tento princip asi ani kvantový počítač nezmění). Klasický počítač vezme prostě tah po tahu, otrocky všechny "zkusí" a ohodnotí výslednou pozici. Jenomže např. už při zahájení je do hloubky 3 tahů asi 9 000 000 možných partií. Kvantový počítač oproti tomu díky superpozici stavů zkoumá všechny možnosti najednou! Při dostatečném počtu qubitů (log[2]x, kde x je celkový počet možností) je tedy nutný počet kroků (zkoušek) roven hloubce prohledávání!
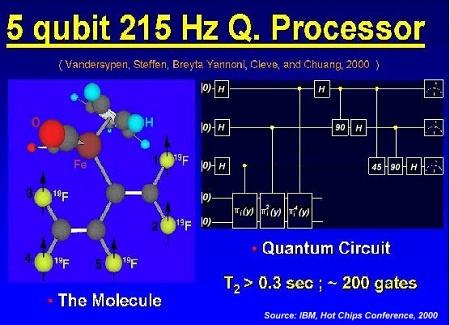
Molekulový a hradlová struktura jednoho z prvních realizovaných kvantových počítačů - 5qubitový IBM z roku 2000.
Základní výpočetní jevy kvantových počítačů
Základem veškerého kvantového počítání a kvantových počítačů jsou následující dva jevy:
-
 Kvantová interference qubitů – vzájemné ovlivňování stavu qubitů, kdy pro některé výpočetní cesty může dojít k vzájemnému vyrušení stavu qubitů, nebo naopak k zesílení pravděpodobnosti jejich stavu (což se využívá v některých kvantových algoritmech). Konkrétně jde o skládání amplitud pravděpodobnosti několika možností. Amplitudy se mohou vyrušit, potom hovoříme o destruktivní interferenci. Pravděpodobnosti dějů jsou pak kvadrátem amplitud pravděpodobností. V praxi při realizaci kvantových počítačů se pak využívá interference vln, tedy skládání vln z několika zdrojů (sčítají amplitudy vln). Jsou-li v protifázi, může dojít k vyrušení výsledné vlny. V detekčním přístroji se detekuje intenzita vlny, která je kvadrátem amplitudy.
Kvantová interference qubitů – vzájemné ovlivňování stavu qubitů, kdy pro některé výpočetní cesty může dojít k vzájemnému vyrušení stavu qubitů, nebo naopak k zesílení pravděpodobnosti jejich stavu (což se využívá v některých kvantových algoritmech). Konkrétně jde o skládání amplitud pravděpodobnosti několika možností. Amplitudy se mohou vyrušit, potom hovoříme o destruktivní interferenci. Pravděpodobnosti dějů jsou pak kvadrátem amplitud pravděpodobností. V praxi při realizaci kvantových počítačů se pak využívá interference vln, tedy skládání vln z několika zdrojů (sčítají amplitudy vln). Jsou-li v protifázi, může dojít k vyrušení výsledné vlny. V detekčním přístroji se detekuje intenzita vlny, která je kvadrátem amplitudy. - Kvantové provázání (propletení) qubitů (entaglement) - zvláštní typ korelace mezi částicemi, kdy dvě provázané částice si vzájemně přejímají svoje vlastnosti. Toho se například využívá i v případě realizace samoopravného systému qubitu. Aktivní složkou je zde pomocný qubit, jenž opraví hodnotu qubitu, na němž došlo k chybě. Např. 3 qubity jsou představovány 1 bitem hlavním a 2 pomocnými. Po jejich propletení dokázal kvantový algoritmus odhalit chybu a opravit ji. Po provedení opravy jsou pomocné bity resetovány pomocí laserového paprsku a mohou tedy fungovat znovu.
Algoritmy vhodné pro řešení kvantovými počítači
I když teoreticky lze kvantové počítání a tedy kvantové počítače využít pro realizaci jakýchkoliv výpočtů, které zvládají i současné počítače, hlavní budoucí využití je pro rychlé výpočty extrémně výpočetně náročných algoritmů, které klasické PC buď není schopné vyřešit nebo v jen velmi velmi dlouhé době (třeba v řádech desítek minut, hodin, dnů či dokonce až roků). Mezi v tomto směru nejznámější patří Shorův algoritmus výpočtu faktoriálu, nebo Groverův algoritmus pro vyhledávání informací v netříděných databázích nebo seznamech.
Příklady některých algoritmů vhodných pro výpočet na kvantových počítačích:
- Hadamard-Fourierova transformace – rychlý výpočet Fourierovy transformace v n-rozměrném prostoru
- Deutsch–Jozsaův algoritmus – pro řešení problému typu černá krabička (black box)
- Simonův algoritmus – pro řešení problému typu černá krabička (black box)
- Shorův algoritmus – nejrychlejší známý diskrétní algoritmus pro výpočet faktorizace. Zatímco doposud ve dvojkové soustavě zapsané číslo má nejlepší dosud nalezený algoritmus výpočtu faktoriálu exponenciální obtížnost, Shorův algoritmus faktorizace postavený na kvantové logice má výpočetní obtížnost zhruba jen kvadratickou. To je právě dáno přirozeným paralelizmem v kvantové logice.
- Odhad Gaussovy sumy - nejrychlejší známý diskrétní algoritmus pro výpočet Gaussovi sumy
- a mnoho dalších...
Logické funkce („hradla“) pro práci s qubity
Podobně jako u klasických počítačů a digitálních systémů lze práci s bity popsat či realizovat prostřednictvím logických funkcí realizujících Boolean algebru, existují podobně i kvantové logické funkce v podobě „kvantových logických hradel“, ze kterých lze „postavit“ strukturu pro kvantový výpočet či realizaci libovolného algoritmu či systému. Hlavní rozdíl klasických logických funkcí a těch kvantových, je fakt, že kvantové logické funkce jsou reverzibilní, tedy nejen ze vstupů lze dostat výstup, ale z výstupu lze přesně získat stavy vstupů. Toto je dáno samotnou podstatou kvantového počítání, takže každá kvantová logická funkce prostě musí být reverzibilní.
Jinak soubor kvantových logických funkcí je výrazně větší než u klasických log. funkcí. To však koresponduje s tím, že u qubitů mimo stavy 1 a 0 zde v kvantové oblastí existuje i superpozice všech možných stavů „mezi tím“, takže tím logicky vyvstávají daleko širší požadavky na aparát zpracování. Například celý soubor základních funkcí NOT, OR, AND, NAND, NOR v kvantové oblastí realizuje jen jedna funkce - Toffoliho hradlo.
Zatím nejznámější „bran“ pro práci s qubity a tedy pro vytváření „obecných zapojení“ kvantových počítačů:
-
 Hadamard hradlo – aplikuje se na jednotlivé qubity, snižuje pravděpodobnosti stavu qubitu |0> nebo |1> na polovinu.
Hadamard hradlo – aplikuje se na jednotlivé qubity, snižuje pravděpodobnosti stavu qubitu |0> nebo |1> na polovinu. - Pauli-X hradlo - aplikuje se na jednotlivé qubity, přetáčí stav qubitu z |0> na |1> a |1> na |0> (ekvivalent funkce NOT u klasických bitů).
- Pauli-Y hradlo - aplikuje se na jednotlivé qubity, přetáčí stav qubitu z |1> na -|1> a ponechává stav |0> na |0>.
- Pauli-Z hradlo - aplikuje se na jednotlivé qubity, přetáčí stav qubitu z |0> na i|1> a ponechává stav |1> na -i|0>.
- Posuvný registr - aplikuje se na jednotlivé qubity, posouvá fázi qubitu stavu |1> o definovaný úhel a ponechává stav qubitu |0>.
- SWAP hradlo - aplikuje se na dva qubity, provádí prohození stavu obou qubitů mezi sebou.
- Řízené hradlo - aplikuje se současně na dva nebo více qubitů, provádí různé maticové operace s qubity.
- Toffoliho hradlo - aplikuje se současně na tři qubity, provádí klasickou boolean algebru s qubity (ekvivalent funkcím OR, AND, NAND, NOR).
- Fredkinovo hradlo - aplikuje se současně na tři qubity, umožňuje realizoval s qubity různé další logické funkce .
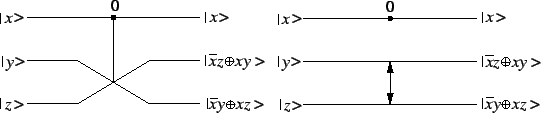
Příklad značení kvantových logických funkcí - zde konkrétně Fredkinova hradla.
Praktická implementace qubitů a tedy i kvantového počítače
Hlavní „nutností“ pro realizaci kvantového počítání je udržení částic ve stavu superpozice (spolu s pozdějším "přečtením" správných dat). Teoreticky kterýkoliv dvouúrovňový kvantově mechanický systém je možné využít pro realizaci qubitu. Kvantová mechanika totiž definuje pro mikrosvět pravidla, které říkají, že lze například speciálně naladěným přesným laserem přenést atom do superpozice základního a excitovaného stavu. Díky tomu může atom uchovávat kvantovou informaci a reprezentovat 1 qubit.
V zásadě jsou aktuálně známé a realizovatelné tři principy pro realizaci jednotlivých qubitů
-
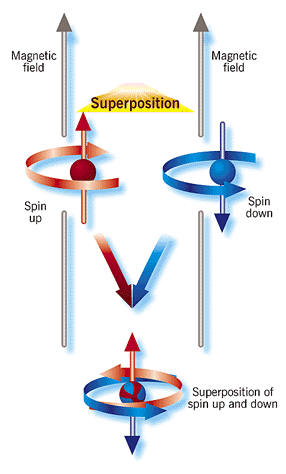 Využití spinu částic (např. elektronů): Spin se dá zjednodušeně interpretovat jako "rotace" dané částice. Každý elektron musí mít nějaký spin - buďto kladný (kladný směr otáčení = 1), nebo záporný (kupodivu záporný směr otáčení = 0). Neexistuje elektron bez spinu. Superpozice stavů můžeme docílit tak, že elektron zasáhneme přesným množstvím záření, které má,zjednodušeně přiblíženo, právě tak akorát energie na zastavení "rotace". Protože však elektron nějaký spin mít musí, existuje 50% pravděpodobnost, že spin zůstane, jak byl, a 50% že se změní. Dokud spin nezměříme (nebo nepřinutíme částici interagovat s vnějším světem tak, aby se spin projevil), trvá superpozice stavů.
Využití spinu částic (např. elektronů): Spin se dá zjednodušeně interpretovat jako "rotace" dané částice. Každý elektron musí mít nějaký spin - buďto kladný (kladný směr otáčení = 1), nebo záporný (kupodivu záporný směr otáčení = 0). Neexistuje elektron bez spinu. Superpozice stavů můžeme docílit tak, že elektron zasáhneme přesným množstvím záření, které má,zjednodušeně přiblíženo, právě tak akorát energie na zastavení "rotace". Protože však elektron nějaký spin mít musí, existuje 50% pravděpodobnost, že spin zůstane, jak byl, a 50% že se změní. Dokud spin nezměříme (nebo nepřinutíme částici interagovat s vnějším světem tak, aby se spin projevil), trvá superpozice stavů. - Využití excitování elektronu (nejlépe atomu vodíku): Nachází-li se elektron na nějakém nižším orbitalu, je možné ho dodáním energie přesunout na orbital vyšší. Pokud dodáme (opět za pomoci záření) přesně hraniční množství energie, je 50% šance na excitaci a 50% na "neexcitaci". Když interpretujeme excitovaný elektron jako 1 a neexcitovaný jako 0, dostáváme opět pro nás příhodnou superpozici stavů.
- Využití polarizace fotonů: Zde můžeme provádět měření roviny polarizace tak, že postavíme fotonu do cesty filtr, kterým se 100% pravděpodobností projdou jen fotony s určitou rovinou polarizace, jejichž stav označíme např. |1>. Fotony polarizované kolmo na rovinu filtru neprojdou vůbec. Ty pak mohou symbolizovat stav |0>. Fotony polarizované v jiných rovinách se budou chovat, jako qubit v superponovaném stavu, kde podle úhlu natočení polarizace se mění amplituda pravděpodobnosti, že foton projde či neprojde filtrem.
Prakticky realizované kvantové počítače
Jeden z prvních opravdu funkčních kvantových počítačů byl postaven již v roce 2000 společností IBM. Jednalo se o 5qubitový počítač pro testovací účely celé technologie.
 Daleko větší „poprask“ pak vznikl v minulém roce (2011), kdy byl celosvětově představen první komerční kvantový počítač D-Wave One, který obsahuje 128qubitový procesor. Rainier, jak se tento kvantový procesor nazývá, pracuje tedy se 128 stavy současně a je vyroben ze supravodivých kovů (niob) chlazených až k hranici absolutní nuly, k čemuž slouží integrované chlazení pomocí tekutého hélia. Konkrétně se využívá Josephova jevu prostřednictvím 24 tisíc Josephsonových smyček. Procesor se programuje pomocí zvláštního programovacího jazyku. Zvládá zatím pouze jedinou matematickou operaci z oblasti diskrétní optimalizace. Procesor je složen celkem z šestnácti menších stejných částí, z nichž každá obsahuje 1500 Josephsonových smyček.
Daleko větší „poprask“ pak vznikl v minulém roce (2011), kdy byl celosvětově představen první komerční kvantový počítač D-Wave One, který obsahuje 128qubitový procesor. Rainier, jak se tento kvantový procesor nazývá, pracuje tedy se 128 stavy současně a je vyroben ze supravodivých kovů (niob) chlazených až k hranici absolutní nuly, k čemuž slouží integrované chlazení pomocí tekutého hélia. Konkrétně se využívá Josephova jevu prostřednictvím 24 tisíc Josephsonových smyček. Procesor se programuje pomocí zvláštního programovacího jazyku. Zvládá zatím pouze jedinou matematickou operaci z oblasti diskrétní optimalizace. Procesor je složen celkem z šestnácti menších stejných částí, z nichž každá obsahuje 1500 Josephsonových smyček.
V budoucí plánu společnosti D-Wave jsou pak i 256qubitové počítače. S nimi pak počítače, které jsou schopné nejen data ukládat v rámci kvantových vlastností částic, ale také zpracovat (logické operace) pomocí kvantových jevů. Cenu by mělo postupně snižovat využití levnějších materiálů. Na začátku letošního roku se už objevily první testy s klasickým křemíkem, byť stále s nutností teploty blížící se k absolutní nule.
Závěrem...
I když se stále vyskytují hlasy, že počítače společnosti D-WAVE jen na oko pracují jako kvantové počítače, a že to nejsou skutečné kvantové počítače, je minimálně z výše uvedeného patrné, že vývoj je v tomto směru již dost daleko. Vždyť již v roce 2000 i společnost IBM realizovala 5qubitový kvantový počítač. Tak či tak, myslím si, že budoucnost kvantového počítání bude světlá. Třeba již za 20 let bude ve velkých vývojářských společnostech a centrech kvantový počítač již samozřejmostí.
Mimochodem již minulý rok bylo oznámeno, že Lockheed Martin, americká společnost podnikající v leteckém průmyslu, zakoupila výše zmíněný kvantový počítač od kanadské firmy D-Wave. Jde o první transakci tohoto typu, tedy koupi a nasazení kvantových počítačů do reálného provozu v komerčním sektoru.
Je samozřejmé, že podobně jako například současně vyvíjené neuronové systémy a počítače nejsou ani kvantové počítače vhodné na všechny možné aplikace. Tak jako neuronové sítě se primárně hodí pro výpočet či řešení aplikací obsahujících velký počet různých vstupních proměnných mezi kterými není jednoznačně daná závislost a zase vůbec se nehodí pro řešení periodických výpočtů, tak naopak kvantové počítače se výborně hodí pro výpočet velmi náročných přesně daných algoritmů a vyhledávání ve velkých databázích, ale vůbec se například nehodí pro potřeby regulace. A nakonec tu paralelně zůstanou i klasické bitové počítače, které prostě nejvíce efektivně řeší jednoduché úlohy, typu „kalkulačka“, přehrávání hudby a videa apod. …
V budoucnu by tak superpočítač měl v sobě obsahovat všechny tři uvedené varianty, a podle aktuální potřeby přidělovat jednotlivým jádrům ty správné úlohy k řešení...
Odkazy na literaturu a články:
- Kompletní podrobný matematický popis a aparát ke kvantovému počítání - http://www.karlin.mff.cuni.cz/~holub/soubory/qc/node1.html
- Popis kvantových bran - http://www.karlin.mff.cuni.cz/~holub/soubory/qc/node18.html
- Nikita Belov: „Kvantové počítače“, prezentace FJFI ČVUT, https://sites.google.com/site/belov222/home/princip-kvantovych-pocitacua
- Petr Kulhánek: „Kvantové počítače“, Aldebaran buletin 21/2003, http://www.aldebaran.cz/bulletin/2003_21_qua.html
- Stránky společnosti D-Wave Systems Inc., výrobce prvních kvantových počítačů - http://www.dwavesys.com , http://www.dwavesys.com/en/dev-tutorial-intro.html
- Článek „The Quantum Computer Is Growing Up: Repetitive Error Correction in a Quantum Processor“ magazínu „ScienceDaily“ - http://www.sciencedaily.com/releases/2011/05/110526141501.htm
- Článek „Quantum Entanglement in Photosynthesis and Evolution“ magazínu „ScienceDaily“ - http://www.sciencedaily.com/releases/2010/07/100721154236.htm
- Článek „Key To Designing Quantum Information Networks: Quantum Memory And Turbulence In Ultra-Cold Atoms“ magazínu „ScienceDaily“ - www.sciencedaily.com/releases/2009/07/090720080904.htm
- Článek „Two Qubits In Action, New Step Towards The Quantum Computer“ magazínu „ScienceDaily“ - http://www.sciencedaily.com/releases/2007/06/070614104042.htm
- Lyza Ziga: "Proposed Quantum Computer Consists of Billions of Electron Spins", http://phys.org/news171705608.html
- Čermák, Kos, Olšina a kol.: „Kvantové počítače“
- http://langsrv.astro.cf.ac.uk/research/research_SQDFWM/SQDFWM.html
- http://sayitwithscience.tumblr.com/post/7384422786/the-qubit-in-computing-is-the-quantum-analog-of
- http://www.nbi.ku.dk/forskningsgrupper/Kvanteoptik/english/qoptlab/research/exp-clock/bloch/
- http://library.thinkquest.org/07aug/01632/qgates.html
- http://claesjohnson.blogspot.cz/2011/05/monstrosity-of-quantum-mechanics-4.html
- http://home.ku.edu.tr/~nwcl/nanoquantum.html
- http://wikis.lib.ncsu.edu/index.php/Quantum_Teleportation






Komentáře
parádní článek
Díky za přiblížení do této problematiky, na zpravodajských serverech je vidět že nikdo z nich netuší o co jde:D ale přesto o tom píšou
Apríl?
Víte, když čtu o kvantových, fuzzy, neuronových a jiných "extra" počítačích, mám pocit, že to pochází z aprílového čísla nějakého (vědeckého) plátku... Tím nechci říct, že "dvojkové" počítače jsou jedinou možnou alternativou. Ale protože se (zatím) uznává zákon zachování hmoty a energie, předpokládám, že něco podobného platí pro i pro informace... Takže můžu vzít páku, aby mě stačila menší síla pro pohnutí objektem, ale zase se o to víc naběhám, abych s tou pákou mohl manipulovat. Podobně v matematice můžu místo násobení použít "jen" sčítání, ale předtím musím operandy zlogaritmovat a pak zase "odlogaritmovat". Předpokládám, že to bude s qubity podobné. Sice vlastní výpočet (možná) bude jednodušší, ale o to složitější bude zadat přesné výchozí podmínky a výsledek opět přesně reprezentovat (kam tedy v tom 36. tahu s tím střelcem vlastně táhnout...). Jinak mám pocit, že výsledky kvantového výpočtu by se daly interpretovat jako "figurka je někde na šachovnici, ale také možná už mimo ni..."
PS: Když vezmu ten příklad náhrady násobení sčítáním logaritmů - tak současným počítačům dá "víc práce" výpočet logaritmů a exponenciály, než to vlastní násobení či dělení, takže si tím "zjednodušením" dost přidáme práci...
:-)
Doporučoval by som preštudovať si kvantovú fyziku, najlepšie knihu Richard Feynman a kvantový svet ... predstava, že elektrón je nejaká malinkatá gulička, ktorá sa niekde nachádza je už veľmi dávno prekonaná. Jasné že platí zákon zachovania hmoty a energie, ale tiež platí že hmota sa može premieňať na energiu a energia na hmotu. A tiež platí Heisenbergov princíp neurčitosti, ten vraví, že vieme zmerať kde sa daná častica nachádza, ale nevieme určiť presne v ktorom okamihu a tiež opačne okamih vieme, ale nie presnú polohu. Oboje sa súčasne určiť nedá. Preto kvantový počítač nepracuje ako klasický so stavmi ANO-NIE ... 0 - 1 , ale s pravdepodobnosťami...pozná aj stavy medzi 0 .. 1.
hmota vs. energie
Můj dotaz bude spíše filosofický než fyzikální (nejsem fyzik), ale nerozumím tomu, jak může být energie non-hmotou a přitom oboje mohou být materiální povahy. Není energie "jen" jiná forma hmoty?
Jinak článek velmi dobrý, díky.
re
Nejsem si jistý, jestli je tohle pravda. Hmota má v sobě nějaký energetický potencionál (E=mc²), ale energii není možné transformovat na hmotu samotnou. Jen pomocí energie můžeme formovat již existujicí hmotu. "Jiná forma hmoty" to podle mě není, protože by v tom případě, měla jít přemět zpátky na hmotu samotnou(Přeměnit energii ve hmotu, ne energií pracovat s již existujicí hmotou). Teď doufám, že jsem nenapsal nějakou hovadinu :).
energie >> hmota
Taky nejsem expert, ale co se přeměny energye na hmotu týče, tak to podle mě jde. Vemte si Velký třesk, při němž e uvolnila pouze energie, ze které potom vnikla veškerá hmota a antihmota a (možná i temná hmota).
V še je energie , hmotu dělá
V še je energie , hmotu dělá rychlost
No hmotu na energii rozbít
No hmotu na energii rozbít můžeš. Nejde ovšem o přeměnu, ale o roztrhání vazeb. Bohužel nejsi schopen ji zpátky složit ve hmotu. Chápu, že rovnice snese všechno, a když odečteš + a potom –, tak dostaneš původní stav. V realitě to tak ale není a tím se liší od odborných představ. Musíš nejdřív realitu pochopit a ne si stavět vzdušné zámky. Pak můžeš realitu popsat. Realita není pravděpodobnost, ale determinismus. Vše má svou příčinu a následek. Například z neschopnosti se dá vytvořit triumf, superpozice. Takový poslanec v parlamentu je i není. Když pak o soustavě nic nevíš, tak nemůžeš určit co se v ní jak pohybuje, Heisenbergov princip neurčitosti. Když ignoruješ rozpory svých tvrzení, tak krom toho, že jsi hlupák, jsi i lhář, protože rozpor znamená omyl a ignorance jej mění ve vědomou lež. A ze lží pravdu nesestavíš.
Je to jinak
No je to taková splácanina. Pane autore, jak se to programuje? Na základě této otázky pochopíte sám,
že jste napsal ptákovinu. Ale obrázky jste převzal pěkné.
Qubitový výpočet realizuje lidská společnost formou trhu.
Hledá tak optimální rozdělení zdrojů.
Prohozená Pauliho hradla
Máte v článku prohozený účinek hradel Pauli Y a Pauli Z. Pauliho Y hradlo mění stav |0> na i|1> a stav |1> na -i|0>; Pauliho Z hradlo ponechává stav |0> a mění stav |1> na -|1>. To lze ostatně vyčíst i z příslušných matic.
faktorizace
Faktorizace je rozklad na prvočinitele, nikoli výpočet faktoriálu.