Jste zde

Úvod do světa napěťové reference – 1. díl

Jan Robenek, 27. Červenec 2009 - 7:21

Tímto článkem otevíráme sérii věnovanou napěťovým referencím a zákeřnostem, které nás mohou provázet při výběru i následném používání jednoho ze základních stavebních kamenů elektronických obvodů.

Napěťová reference – k čemu je to dobré?

Jako lidé jsme byli vybaveni nejrůznějšími pocity, které v nás okolní prostředí může vyvolávat. Celou řadu vjemů již dokážeme analyzovat, buď vlastními schopnostmi nebo ještě přesněji elektronickou cestou, přičemž to co stále ještě měřitelné není se usilovně snažíme měřitelným učiniti. A tak jsme vytvořili obraz okolního světa, který pracuje s napěťovými výstupy nejrůznějších čidel, nesoucími celou řadu informací, třeba o teplotě vody v bazénu nebo množství kraválu po 22 hodině, které může být s teplotou vody v přímé úměře. Hodnověrné zpracování však bude vyžadovat neméně spolehlivý porovnávací standard, který v tomto případě již nenazýváme osobní zkušeností či mírou znechucení ale napěťovou referencí. Otázkou pro návrháře tak není zdalipak referenci použije, ale spíše která z nich bude pro daný účel nejvhodnější.

Jednoduše řečeno, pod označením napěťová reference budeme hledat součástku nebo rovnou celé obvodové řešení, zajišťující známý, dostatečně neměnný potenciál a to tak dlouho, jak to jen příslušný systém bude vyžadovat – několik minut, hodin nebo i dlouhých let. Potřebuje – li naše zařízení informaci z okolního světa, např. o velikosti napětí na baterii, tekoucím proudu, výkonové spotřebě, velikosti a povaze signálu nebo identifikaci vzniklé chyby, bude příchozí signál porovnávat s daným standardem. Každý komparátor, A/D převodník, D/A převodník nebo detekční obvod proto vybavíme napěťovou referencí, která tuto funkci s radostí zajistí. Vzájemným porovnáním měřeného napětí se známou hodnotou lze dostatečně přesně vyhodnotit velikost jakéhokoli signálu.

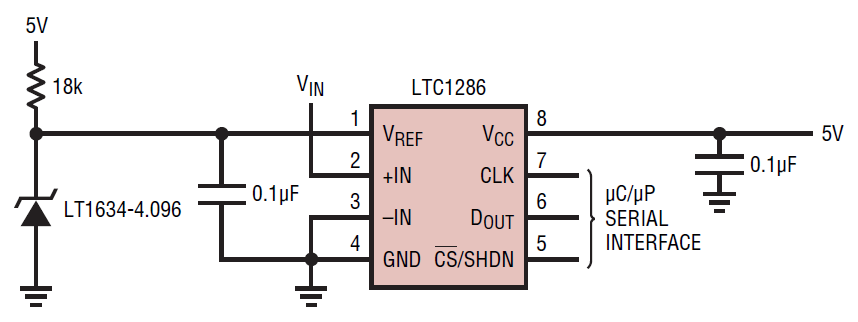
Typické použití napěťové reference během A/D převodu

Které vlastnosti referenci definují?

Ikdyž lze s ohledem na dané specifické vlastnosti reference vyrábět různými způsoby, nejdůležitějšími vlastnostmi při dosahování známého výstupního napětí stále zůstávají přesnost a stabilita. Odchylku od takto vymezené úrovně pak nazýváme chybou. Specifikace napěťové reference k vyčíslení povolených tolerancí při známých okolních podmínkách obvykle užívají následujících parametrů:

Počáteční přesnost
Teplotní drift
Dlouhodobá stabilita
Teplotní hystereze

1) Výchozí, někdy také počáteční přesnost (Initial Accuracy)

Jedná se o rozdíly ve výstupním napětí, měřené na dané teplotě, obvykle při + 25 °C. Ikdyž se výchozí napětí výstupu může s každým obvodem měnit, a taky se obvykle mění, bude – li pro daný jeden kus konstantní, lze s tím jednoduše počítat a případný posun vyrovnat kalibrací. (Bude – li např. jmenovité výstupní napětí + 5 V a tolerance ± 0.005 V, musíme počítat s rozptylem v rozmezí + 4.995 V až + 5.005 V. Referenční napětí tak po zapnutí napájení může při pokojové teplotě dosahovat např. + 4.996 V = konst. Lze ale předpokládat, že se bez dalších vlivů a při vhodném vf blokování nebude z tohoto titulu dále svévolně pohybovat ve výše vymezeném rozmezí. Trvalou výchozí odchylku o – 0.004 V, která např. mohla přímo ovlivnit vstupní rozsah použitého A / D převodníku, v tomto případě jej úměrným způsobem zmenšila, tak dokážeme ošetřit vhodnou kalibrací.)

2) Teplotní drift (Temperature drift)

Tato velmi často užívaná specifikace vyjadřuje, jakým způsobem se bude výstupní napětí měnit s nepřítelem č. 1 pro vše polovodivé – teplotou. Za teplotní drift můžeme poděkovat nedokonalostem polovodičové struktury v zásadní kombinaci s nelinearitami samotného referenčního prvku. Protože jsme se již museli naučit řešit i složitější případy, jistě nás nepřekvapí častá nelineární povaha driftu, při které stejným teplotním krokům nemusí pokaždé odpovídat stejně velké změny napěťového výstupu.

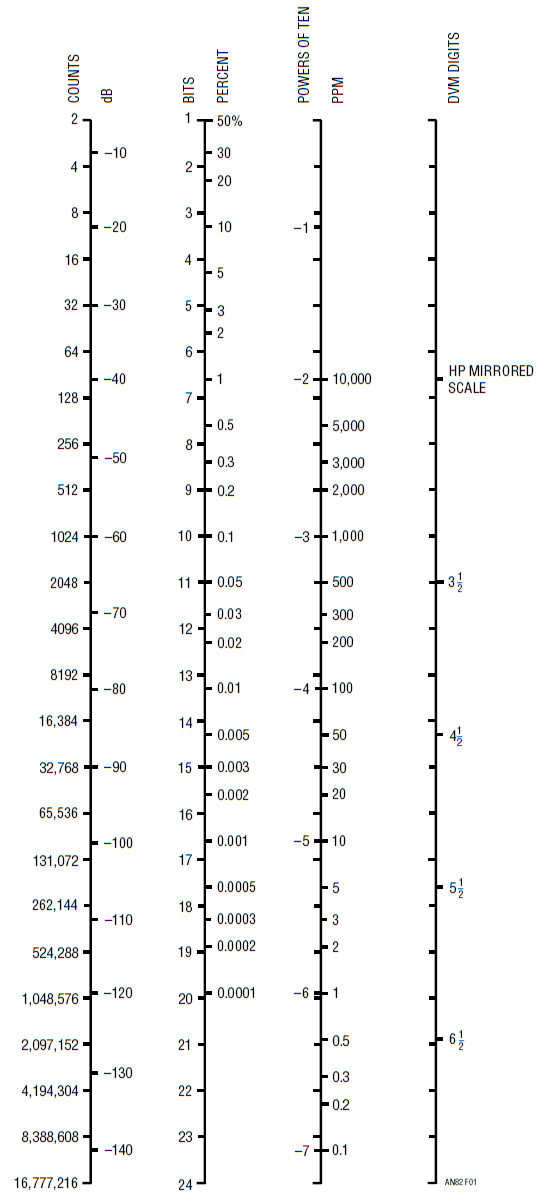
Pro mnoho součástek se stal teplotní drift, někdy také jako teplotní koeficient TC, vyjádřený v jednotkách ppm/°C, hlavním zdrojem chyby, kterou je potřeba zohlednit, pokud možno i kalibrací. (Protože si vážíme i začínajících čtenářů – elektroniků, budu si s laskavým přimhouřením oka zkušenějších vývojářů dovolovat další malé odbočky: Velikost 1 ppm vychází z celého svého označení, tj. part per million a tvoří tak jednu milióntinu určitého množství. Bude – li např. mezi jedním miliónem lineárních obvodů 7805 deset vadných, rozumíme tím 10 ppm nepoužitelných kusů. Jednoduchým porovnáním pak dojdeme k následujícímu výsledku: 1 ppm = 0.000 001, 1 % = 0.01, 1 ppm proto bude rovno 0.000 1 %. Bližším určením jednotky, tj. ppm/°C, vyjadřujeme míru, o kterou naše referenční napětí může popojet s 1 °C.)

Často se však setkáváme s nesprávně zažitou představou, která nám mylně nalhává, že teplotní drift lze vždy považovat za lineární. Taková domněnka pak může lehce svádět ke scestným názorům typu: „Na menším teplotním rozsahu bude výstupní drift rovněž menší.“ Přitom opak je mnohokrát pravdou. Teplotní koeficient je totiž obecně tvořen vypočítanou hodnotou, založenou na minimální a maximální velikosti napětí, bez ohledu na teploty, při kterých bylo těchto extrémů dosaženo. Pro napěťové reference, které ve svém vymezeném teplotním rozsahu vykáží „dostatečně“ lineární odezvu, případně také u aplikací s ne tak silným požadavkem na přesnost, lze největší definovanou chybu úměrně přiřadit celému teplotnímu rozsahu. Je to proto, že maxima a minima výstupního napětí budou obvykle k nalezení na maximech a minimech provozních teplot. Pro velmi přesné reference, často jednoznačně rozpoznatelné svým velmi nízkým teplotním driftem, naopak může dominovat právě nelineární povaha celého problému.

Reference s teplotním koeficientem 100 ppm/°C se tak může docela dobře jevit zcela lineární v celém rozsahu provozních teplot, protože samotná velikost driftu zastíní výchozí nelinearity. Na druhé straně referenční zdroj, definovaný velikostí driftu 5 ppm/°C již nelineární povahu nemusí umět zamaskovat a je potřeba ji vhodně zohlednit.

Příklady teplotních charakteristik napěťových referencí

Situaci vhodně přibližuje zobrazená závislost výstupního napětí v podobě dvou možných teplotních charakteristik. Nekompenzovaná bandgap reference se zde bude jevit jako parabola s minimy na příslušných teplotních extrémech a maximem ve středu svého rozsahu. Na druhé straně, teplotně kompenzovaná bandgap reference, např. LT1019, bude svou závislostí spíše připomínat křivku tvaru písmene S, přičemž zásadní zvrat se bude při zahřívání opět odehrávat v oblasti středu zkoumaného teplotního rozsahu. Celková přesnost ale dozná výrazného zlepšení.

(Jak bylo dosaženo barevně vyznačených ploch na předchozím obrázku? Tak nejdříve plný teplotní rozsah a 10 ppm/°C: Teplota nabývá hodnot od -50 °C až do +125 °C, tj. celkem 175 °C. Máme – li pracovat s odchylkou 10 ppm/°C, dostaneme na celém rozsahu 10 ppm/°C x 175 °C = 1750 ppm, tj. 1750 / 1 000 000 = 0.001 75. Výsledek nyní zmenšíme na polovinu, protože chyba může dosahovat jak kladných, tak i záporných úrovní. Dostaneme tedy 0.001 75 / 2 = 0.000 875. K dispozici máme výstupní napětí v normovaném tvaru, ale není problém si zde představit i konkrétní referenční napětí. V případě normovaného napětí 1.000 V tak získáváme pro celý teplotní rozsah a definovanou odchylku 10 ppm/°C následující toleranční pásmo 1.000 ± 0.000 875 V, které přesně odpovídá vyznačeným mezím grafu. Stejným způsobem se pak dopracujeme i k přípustné toleranci v rámci ohraničeného teplotního rozsahu 0 °C až 70 °C při teplotním driftu 5 ppm/°C. Pro námi diskutovaný příklad dostáváme 1.000 ± 0.000 175 V. Jednoduché, že?)

Jednoduchý způsob převodu mezi různými způsoby matematického vyjadřování

Nejlepším způsobem práce s definovaným teplotním driftem tedy zůstává určení maximální velikosti celkové chyby v rámci stanoveného teplotního rozsahu. Zároveň však musíme při dílčích úvahách počítat i s možnou nelineární povahou celé závislosti.

3) Dlouhodobá stabilita (Long Term Stability)

Tímto parametrem výrobce definuje způsob „stárnutí“ daného čipu a jeho sklon ke změnám referenčního napětí v čase, nezávisle na dalších proměnných. Počáteční posuny bývají z velké části způsobeny mechanickými změnami a vnitřním pnutím samotné součástky, včetně použitého čipu. Ve výsledku se takové namáhání může projevovat rozsáhlejšími výchozími změnami, které se však s postupem času rychle vytrácí. Počáteční drift v sobě také zahrnuje změny elektrických vlastností jednotlivých obvodových prvků včetně samotného ustálení až na atomární úrovni. Dlouhodobé změny mají rovněž svou příčinu v odchylce od původních elektrických vlastností. V tomto případě již ale hovoříme spíše o stárnutí. Takový drift se pak bude v průběhu času ve srovnání s počátečním driftem jevit jako méně výrazný. Nelze se tedy divit, že bývá často vyjadřován jako drift / √(kHr). Napěťové reference budou při vyšších teplotách stárnout výrazně rychleji.

(Jak pracovat s vyjádřením drift / √(kHr) ? Budu – li mít zcela obecně dlouhodobou stabilitu 300 ppm / √(kHr), dostávám tím zároveň informaci, že se např. za jeden rok odchýlím o 888 ppm a za deset let o 2 809 ppm. Číslo 2 809 přitom není 10násobkem výchozího 888. Udělal jsem někde chybu? Nikoli, za vše může odmocnina, odrážející nelineární ujíždění zkoumaného parametru během stárnutí obvodu. Tak tedy: K výpočtu velikosti driftu během stanoveného časového období musíme

zvolený čas převést na tisíce hodin (kHr)
odmocnit
vynásobit velikostí driftu

Budeme počítat společně. Jestliže jeden rok trvá přibližně 8.77 kHr (počítáme i s těmi přestupnými jednou za 4 roky, tj. 365.25 dnů x 24 hodin = 8 766 hodin) po odmocnění dostaneme 2.961 4. Vynásobíme – li tento údaj velikostí 300 ppm, dostaneme po zaokrouhlení dolů 2.961 4 x 300 ppm = 888 ppm, což vyjadřuje odchylku po jednom roce. Pokud nás bude zajímat období 10 let, tj. 87.7 kHr, dostaneme stejným způsobem 2809 ppm. Obvod již nestárne tak rychle, ale záleží na teplotě, při které bude provozován. A jak to bude v případě, kdy nebude čip nějakou dobu vůbec pod napětím? Takový odpočinek může stárnutí výrazně zpomalit. V našem modelovém případu tak můžeme uvažovat třeba 1 / 10 driftu při zatížení, tj. 30 ppm / √(kHr). Vždy však bude záležet na konkrétní situaci.)

4) Teplotní hystereze (Thermal Hysteresis)

Tato mnohdy přehlížená specifikace může v celé řadě případů vytvářet dominantní zdroj celkové chyby napěťové reference. Opět se jedná o zcela přirozenou vlastnost, která pouze odráží různé teplotní namáhání čipu v důsledku jednotlivých cyklů. Vůči svému okolí se hystereze projevuje změnou výstupního napětí při dané teplotě, následující po cyklu s větší tepelnou náročností. Parametr sice nevykazuje závislost na teplotním koeficientu či časovém driftu, přesto ale dokáže snížit účinnost výchozí napěťové kalibrace.

Většina referencí má snahu během následujícího teplotního cyklu pohybovat se svým napěťovým výstupem okolo jeho jmenovité úrovně, takže lze teplotní hysterezi obvykle vymezit předvídatelnou maximální hodnotou. Aby to však nebylo zase tak jednoduché, má každý výrobce svou vlastní metodu k určení zmiňovaného parametru, což může v případě typických hodnot působit poněkud zavádějícím způsobem.

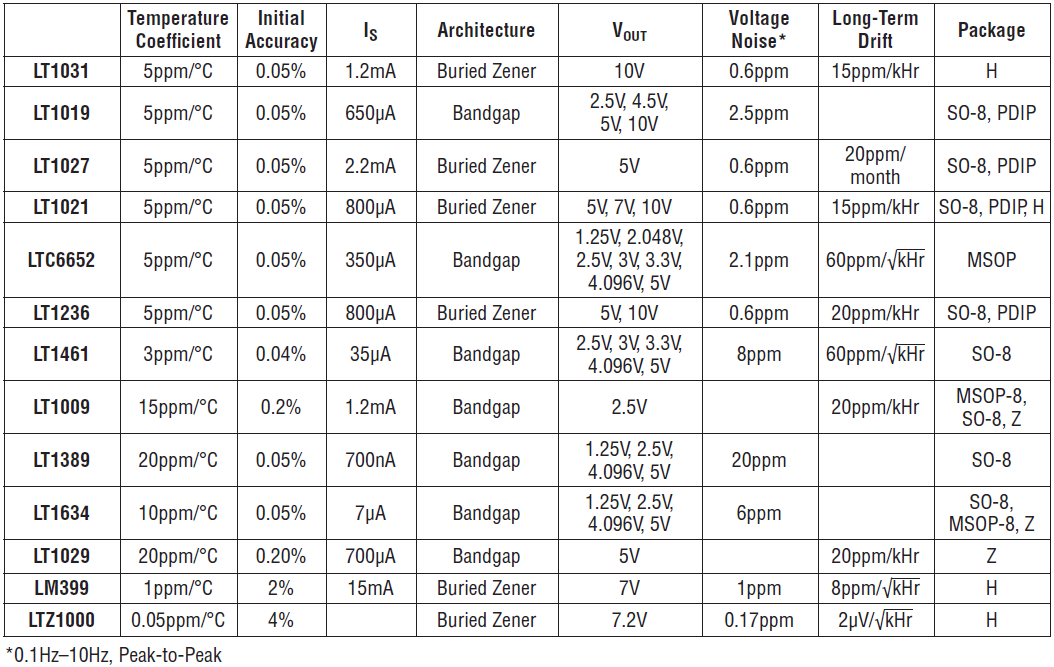
Specifikace některých napěťových referencí

Některé další specifikace

V závislosti na požadavcích konkrétního zapojení nás mohou v souvislosti s napěťovou referencí zajímat i další parametry, např.

Napěťový šum (Voltage Noise)
Kolísání výstupního napětí v závislosti na velikosti napájecího napětí (Line Regulation / PSRR)
Kolísání výstupního napětí v závislosti na proudovém odběru zátěže (Load Regulation)
Úbytek napětí mezi vstupem a výstupem (Dropout Voltage)
Napájecí rozsah (Supply Range)
Proudový odběr (Supply Current), resp. také výstupní proudová zatížitelnost

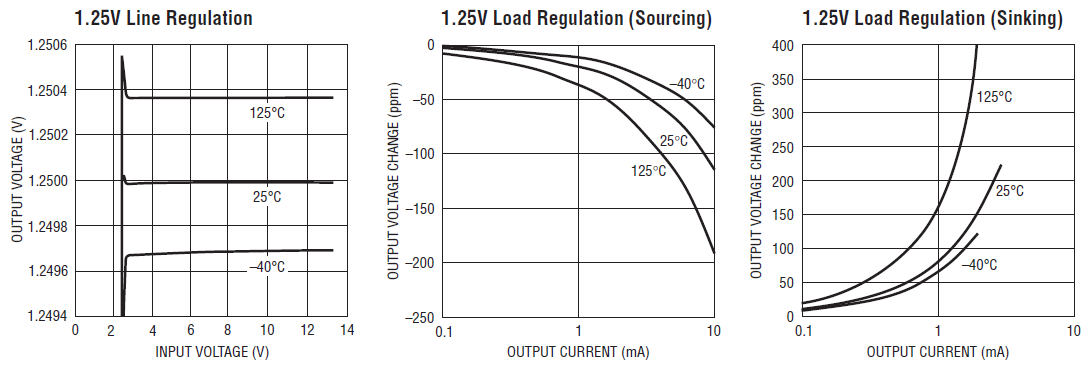
Konkrétní příklad Line / Load regulace pro LTC6652

(Pochopitelně nás bude také zajímat jmenovité výstupní napětí, které sice lze dodatečně upravovat, ale každá taková úprava do zapojení vnáší nejednu další chybu. Příkladem může být referenční napětí, které jednak definuje rozsah A / D převodníku a zároveň po vhodném dělení a impedančním oddělení vytváří „střed“ měřeného signálu při nesouměrném napájení celého zařízení.)

Závěr:

Každá volba napěťové reference znamená určitý kompromis, minimálně mezi dosaženými parametry a cenou, kterou za ně platíme. Tato série článků se proto ve svém 1. dílu pokusila pro tyto účely definovat a vymezit základní parametry, které nelze jen tak beztrestně přehlížet. Příště zaměříme svou pozornost na jednotlivé typy a jim příslušející obvodová řešení zdrojů referenčního napětí.