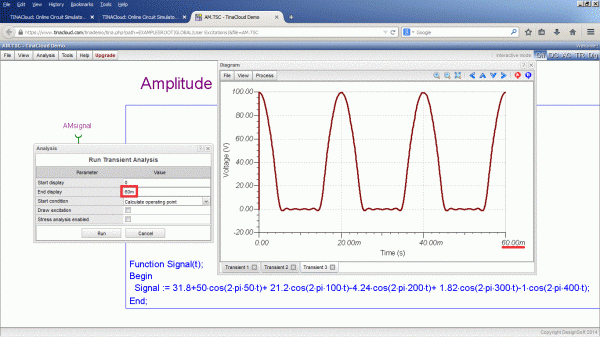
Simulační program TinaPro (Tina) má nověji i internetovou verzi TinaCloud. Ta je sice od nejnovější ostré free deváté verze Tina-TI nepoužitelná na simulaci obvodů, ale harmonická analýza či syntéza se s ní demonstrovat dá. Navíc konečně byla opravena záměna stupňů za radiány, takže kromě složkového tvaru řady (A_k,B_k) řady jsou nyní přepočítány správně i tvary s fázovým posuvem (D_k,fi). Oproti zvyklostem je dána přednost funkci kosinus pro zápis řady místo častější varianty součtu sinusovek (C_k,fi). Po spuštění simulátoru volbou Free Trial je zapotřebí kliknutím vybrat v galerii zapojení obvod s amplitudovou modulací.

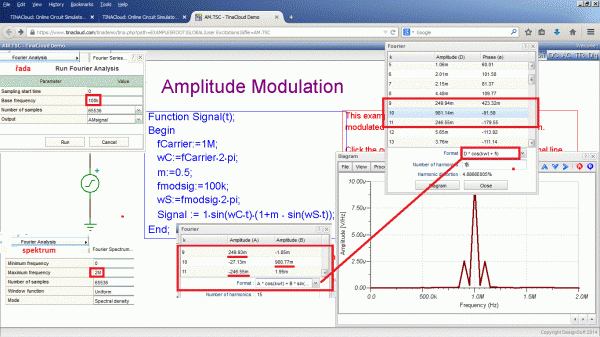
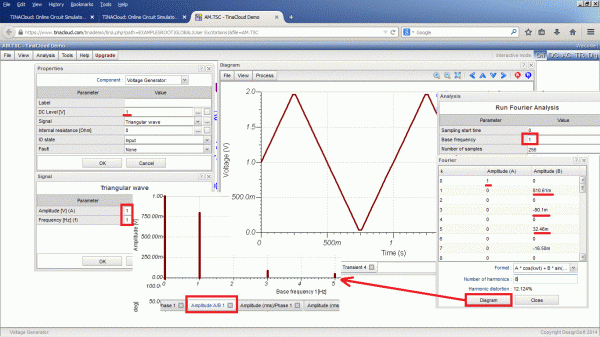
Průběh se vykreslí klasicky volbou přechodové analýzy Analysis-Transient-Run. Z matematického zápisu signálu okopírovaného na ploše je zřejmé, že AM signál má nosnou 1 MHz a modulační 100 kHz. Tomu odpovídá spektrum s postranními složkami 900 kHz a 1 100 kHz. Toto spektrum modulované vlny si lze znázornit pomocí Fourierovy analýzy. Hezčí obrázek dává volba Analysis-Fourier Analysis-Fourier spektrum s nastavením maximum frequency 2M a Window function Uniform s mode Spectral density. Je možné zvětšit přesnost výpočtu Number of samples až na 65 536 vzorků. Po zobrazení spektra AM je možné ještě kliknutím na okno grafu upravit tloušťku čáry Width 3 a vodorovnou osu Upper limit 2 s Precision 1. Tím se získá klasický obrázek spektra AM signálu s nosnou a horním a dolním pásmem (pro jednu sinusovku) se správným poměrem jednotlivých složek. Hloubka modulace zvolená v modrém zápisu signálu byla zvolena na 0,5 a postranní pásma tedy budou mít m/2 krát amplituda nosné (10u a 2,5u). V obrázku lze kurzory odečítat a zkontrolovat tak kmitočty. Pokud nás ale zajímají velikosti amplitud a ne spektrální hustota, je vhodnější zvolit druhou volbu Analysis-Fourier series. Pokud se nastaví základní Base frequency na 100k, tak hledané harmonické složky budou mít pro tento signál pořadí 9,10 a 11. Takže je zapotřebí zvětšit po proběhlém výpočtu v dialogovéme okně Number of harmonics třeba na 15. Pro zpětnou syntézu bude vhodnější přepnout tvar řady do složkového zobrazení. Pak není třeba přepočítávat stupně na radiány.

Podtržené hodnoty z obr. 2 lze použít pro zpětnou syntézu průběhu, což po zaokrouhlení dá řadu:

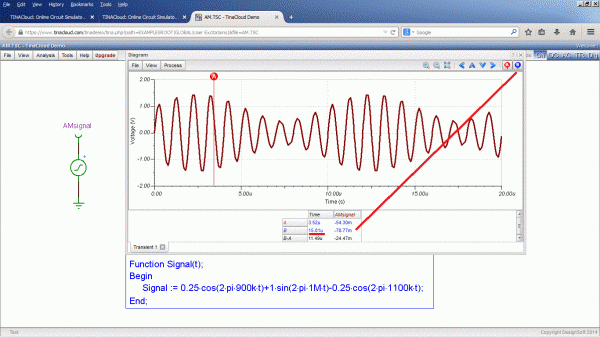
Signal := 0.25*cos(2*pi*900k*t)+1*sin(2*pi*1M*t)-0.25*cos(2*pi*1100k*t); .

Pokud se tato Fourierova řada zapíše po kliknutí na symbol zdroje do dialogového okna User defined fiction - …- Function signal(t); -… místo předchozí definice, zobrazí se shodný průběh s původním. Text definice průběhu lze přepsat i do informativního okénka na ploše. Nejde s ním sice posouvat, ale je možné jej dostat odřádkováním do volného místa obrazovky. V zobrazeném průběhu (Transient) lze odečítat pomocí kurzorů. Zobrazil se mi sice jen kurzor A, ale zadáním hodnot do dialogového okna pod průběhem odečítá i nezobrazený kurzor B. Ale u jiných zapojení se zobrazily oba kurzory.

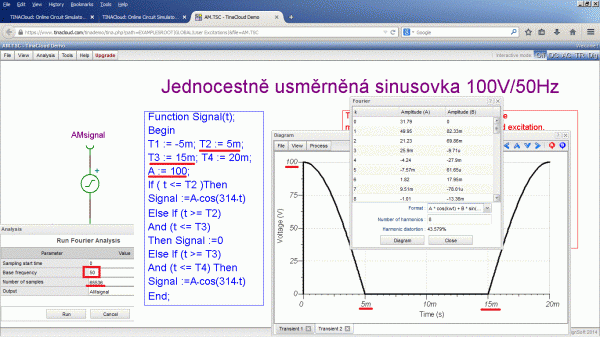
Program má tendenci se kousat, takže před dalším příkladem je vhodné vrátit se k výchozímu nastavení volbou File – Revert to original. Jednocestně usměrněný průběh 100 V/50 Hz lze pro jednu periodu zapsat po částech zápisem (střídají se úseky kosinus a nula):

Function Signal(t);

Begin

T1 := -5m; T2 := 5m;

T3 := 15m; T4 := 20m;

A := 100;

If ( t <= T2 )Then

Signal :=A*cos(314*t)

Else If (t >= T2)

And (t <= T3)

Then Signal :=0

Else If (t >= T3)

And (t <= T4) Then

Signal :=A*cos(314*t)

End;

Při Fourierově analýze je nutné opět nastavit kmitočet základní harmonické (50 Hz) a doporučuji zvětšit přesnost výpočtu zvětšením počtu vzorků na maximum (65 536).

Hodnoty lze přes schránku okopírovat CTRL A a CTRL C a vložit do textu CTRL V.

Metoda je to numerická a hodnoty, které jsou výrazně menší, jsou jen chybou výpočtu. Takže výsledná řada bude mít jen kosinové složky (byla schválně zadána jako funkce sudá) s hodnotami: 31,8 V, 50 V/50 Hz, 21,2 V/100 Hz, -4,24 V/200 Hz, 1,82 V/300 Hz, -1 V/400 Hz. Opět přes File – Revert to originál lze zkontrolovat řadu zpětnou syntézou zápisem do uživatelsky definované funkce:

Signal := 31.8+50*cos(2*pi*50*t)+ 21.2*cos(2*pi*100*t)-4.24*cos(2*pi*200*t)+ 1.82*cos(2*pi*300*t)-1*cos(2*pi*400*t);

Nepřesnost numerického výpočtu analýzy se liší průběh od průběhu. Například u jednoduchého posunutého trojúhelníku vyjde výpočet naprosto přesně i při malém počtu vzorků. Spektrum ze spočítané řady se vykreslí volbou Diagram. Pak je zapotřebí ještě vybrat z vykreslených spekter to správné (Amplitude A/B). U tohoto diagramu nelze volit tloušťku čáry a tak v následujícím obrázku byly úsečky spektra obtaženy v programu Malování. Tento program byl zvolen jako grafický výstup kopií obrazovky (PrtSC).

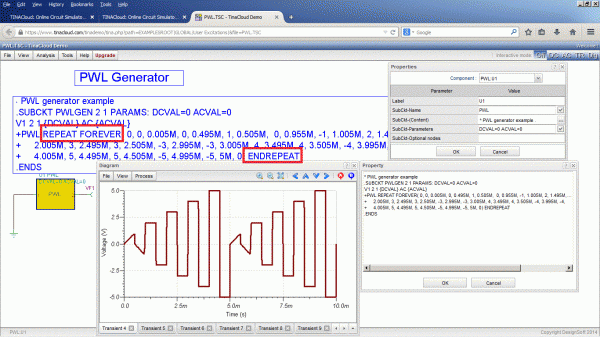
V nabídce volby zdrojů je kromě sinus/cosinus, trojúhelníku, obdélníku, pulzů a uživatelsky definovatelných průběhů možnost zadávat i PWL zdroj. Ten lze využít pro zápis libovolného průběhu pomocí tabulky hodnot x/y (napětí/čas) podobně jako to bylo realizováno při simulaci x/y projektoru. Pro lepší pochopení Piecewise linear source je vhodnější otevřít další obvod (makro) demoverze PWL generátor se zadáním průběhu:

* PWL generator example

.SUBCKT PWLGEN 2 1 PARAMS: DCVAL=0 ACVAL=0

V1 2 1 {DCVAL} AC {ACVAL}

+PWL REPEAT FOREVER( 0, 0, 0.005M, 0, 0.495M, 1, 0.505M, 0, 0.955M, -1, 1.005M, 2, 1.495M, 2, 1.505M, -2, 1.995M, -2,

+ 2.005M, 3, 2.495M, 3, 2.505M, -3, 2.995M, -3, 3.005M, 4, 3.495M, 4, 3.505M, -4, 3.995M, -4,

+ 4.005M, 5, 4.495M, 5, 4.505M, -5, 4.995M, -5, 5M, 0) ENDREPEAT

.ENDS

Zápis byl upraven o nekonečné opakování průběhu (REPEAT FOREVER a ENDREPEAT)

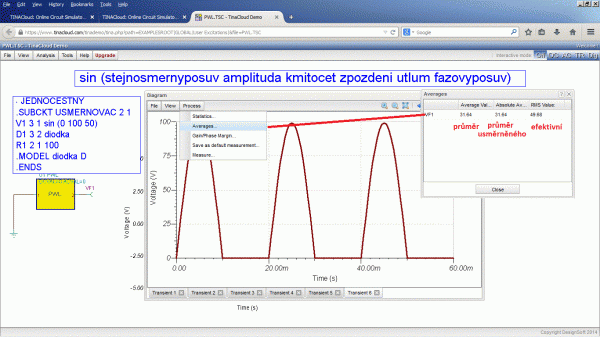
Po částech lineární zdroj PWL byl vložen do podobvodu (subcircuit). Do podobvodu lze ale vložit i netlist libovolného zapojení. Takže lze zkusit vygenerovat jednocestně usměrněný průběh mnohem jednodušeji zapojením jednocestného usměrňovače. Škoda jen, že nelze rozmítat kmitočet nebo stejnosměrnou hodnotu zdroje umístěného uvnitř podobvodu. V opačném případě by bylo možné realizovat i stejnosměrnou a střídavou analýzu jednoduchých obvodů zapsaných textovým zápisem obvodu – netlistem.

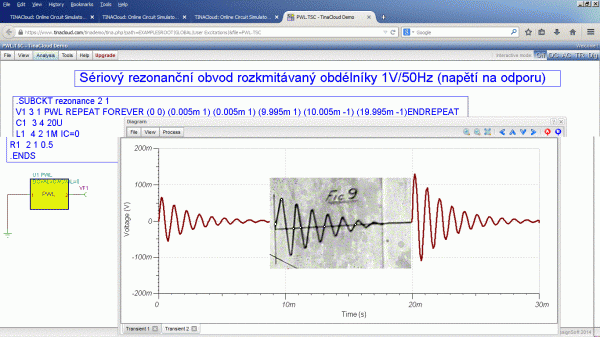
V okně grafu lze realizovat i měření průměrné hodnoty signálu, průměrné hodnoty absolutní hodnoty signálu a efektivní hodnoty signálu. Při výpočtu Fourierovy řady se navíc zobrazuje činitel harmonického zkreslení k (THD Total Harmonic Distortion). Na závěr je možné zkombinovat zápis definovaného zdroje a obvodu a odsimulovat tak průběh z úlohy sto let staré.

Protože při zápisu netlistu obvodu se snadno udělá chyba (závorky, středníky), tak pro případné experimenty je netlist uveden pro okopírování do schránky:

.SUBCKT rezonance 2 1

V1 3 1 PWL REPEAT FOREVER (0 0) (0.005m 1) (9.995m 1) (10.005m -1) (19.995m -1) ENDREPEAT

C1 3 4 20u

L1 4 2 1M IC=0

R1 2 1 0.5

.ENDS