Hlavní kouzlo zpětnovazebních zesilovačů spočívá v tom, že pokud je původní zesílení zesilovače bez zpětné vazby dostatečně velké (dnes se dosahuje i milionu), tak už na jeho hodnotě nezáleží a vlastnosti nového zapojení se zpětnou vazbou pak určuje pouze zpětná vazba, kterou tvoří nejčastěji dva odpory. Jako bonus zpětná vazba zmenší zkreslení, zvětší šířku pásma a změní vstupní a výstupní impedance zesilovače a to v poměru, kolikrát zpětná vazba zmenšila původní zesílení. A pokud ve zpětné vazbě budou kondenzátory, získají se aktivní filtry, když nelineární prvky, tak nelineární zesilovače. Možnosti této koncepce jsou opravdu veliké a návrh zesilovače je přitom jednoduchý, protože se redukuje na návrh zpětné vazby.
Obr. 1: Stabilized Feedback Amplifiers by H. S. Black, 1934 [5]
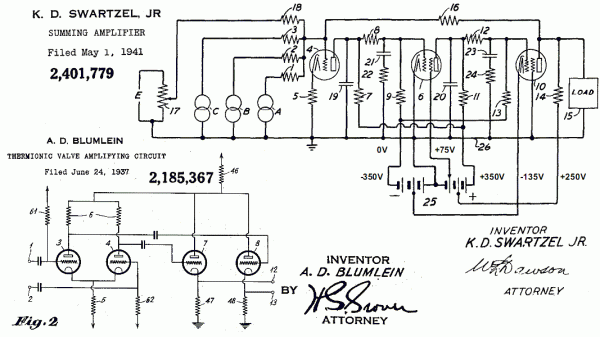
Základní bloky pro konstrukci operačního zesilovače z elektronek byly známy už před druhou světovou válkou. A. D. Blumlein vynalezl kromě rozdílového zesilovače i binaural sound, tj. dnešní stereofonii. Umřel mladý za války v roce 1942 v havarovaném letadle Halifax V9977 při testování leteckého radaru (klystron, magnetron) [7].
Obr. 2: Elektronkový rozdílový (A. D. Blumlein) a součtový zesilovač (K. D. Swartzel)
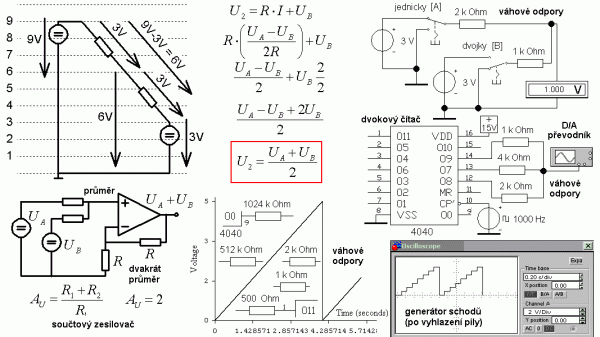
Nejjednodušší matematickou operací je součet. Na to v principu stačí aplikovat Kirchhoffovy zákony a spojit dva napěťové zdroje do série, jako když se nastavuje pracovní bod zesilovače, anebo spojit „neexistující“ proudové zdroje paralelně. Nejelegantnější je ale odporový směšovač, kdy se přes stejné odpory propojí dva zdroje proti sobě. Uprostřed bude průměr napětí a to není nic jiného, než dvakrát zmenšený součet. Takže pak už jen stačí připojit zesilovač s dvojnásobným zesílením a tím získáme součtový zesilovač. Na stejném principu, jen spojením váhových odporů (1, 2, 4, 8…), lze sestrojit nejjednodušší D/A převodník, což je demonstrováno na generátoru schodů s dvojkovým čítačem 4040.
Obr. 3: Průměrovací směšovací obvod a jednoduchý D/A převodník z váhových odporů
Analogový počítač se dnešním číslicovým nepodobá ani vzdáleně. Jeho úlohou bylo zpravidla vyřešit nějakou regulaci, nebo odsimulovat nějaký přechodový děj a to na základě transformací (analogií), třeba mechanický či tepelný děj, a popřípadě vyřešit soustavu diferenciálních rovnic. Prostě se sestavilo nějaké zapojení a přístroj odměřil nebo zakreslil výsledný průběh napětí. Oproti nastupujícím číslicovým počítačům byla jeho výhodou rychlost. Přivedlo se napětí například na integrátor a na výstupu byl okamžitě integrál vstupního průběhu. Nevýhodou samozřejmě byla nedostatečná přesnost a složité zadávání řešeného problému. Dobrou představu práce s analogovým počítačem dává obrázek z návodu ke stavebnici analogového počítače Heathkit H1 [8].
Obr. 4: Stavebnice analogového počítače Heathkit analog computer H1 1956 [8]
Toto počítačové monstrum mělo sedmdesát elektronek a část z nich byla vystrčena kvůli chlazení a možná i kvůli estetice ven a k dispozici tak bylo 15 počítacích zesilovačů. U nás vyráběla polovodičové analogové počítače MEDA Aritma Praha a spousta fotografií analogových počítačů včetně tohoto simulátoru auta je na stránkách [9].
Obr. 5: Analogový simulátor řízení auta (small analog steering simulator) 1958 [9]
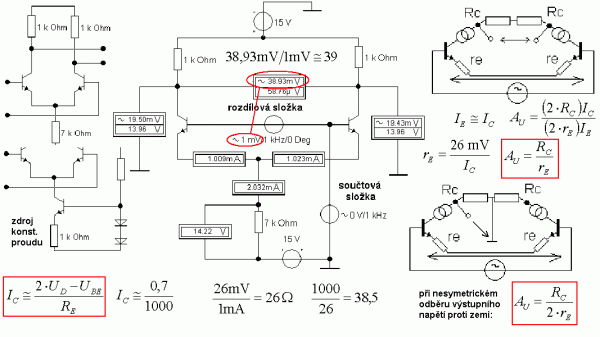
Základem většiny operačních zesilovačů a velké části zesilovačů obecně je vstupní rozdílový stupeň. Umožňuje totiž snadno zavést celkovou zpětnou vazbu a dá se postavit i bez vazebních kondenzátorů, takže může zesilovat i stejnosměrné napětí. Navíc zesiluje pouze rozdíl mezi vstupy a tím je principiálně teplotně nezávislý a odolný proti symetrickému rušení. Zpravidla mívá v emitoru velmi velký zpětnovazební odpor anebo dokonce tranzistorový proudový zdroj, takže bude mít i extrémně velký vstupní odpor. Prostě je to ideální řešení vstupního obvodu zesilovače.
Obr. 6: Odvození zesílení rozdílového stupně metodou beta bariéry
Zkušební simulační zapojení má mezi báze zapojen vstupní rozdílový signál (1 mV) a pro případnou kontrolu netečnosti k souhlasnému signálu má i společnou součtovou složku mezi báze a zem (0 V). Odvozený vzorec pro zapojení se symetrickým výstupem je shodný se vztahem pro nezatížený tranzistorový stupeň SE bez zpětné vazby. Zapojení připomíná Wheatstonův můstek pro měření odporů. Pokud budou tranzistory stejné a to na polovodičovém čipu budou, tak se proud rozdělí rovnoměrně do obou větví můstku. Můstek zůstane vyvážen i v případě, že se na báze obou tranzistorů přivede shodné napětí, protože tranzistory se sice pootevřou, ale oba stejně, takže dělicí poměr větví můstku bude opět stejný. Místo galvanometru můstku je výstup zesilovače a bude tam nulový rozdíl napětí. Pokud ale bude mezi bázemi rozdíl napětí, jeden z tranzistorů se otevře víc, jeden míň a můstek se rozváží a rozdíl se zesílí. Pokud se obvod nastaví tak, že protékající proudy větvemi a společným emitorovým odporem vytvoří napětí právě tak akorát, aby báze byly při symetrickém napájení na potenciálu země, není třeba ani odpory do bází a tím pádem ani vazební kondenzátory a zesilovač bude zesilovat i velmi malá napětí, bez odporu do báze pro otevření přechodu PN.
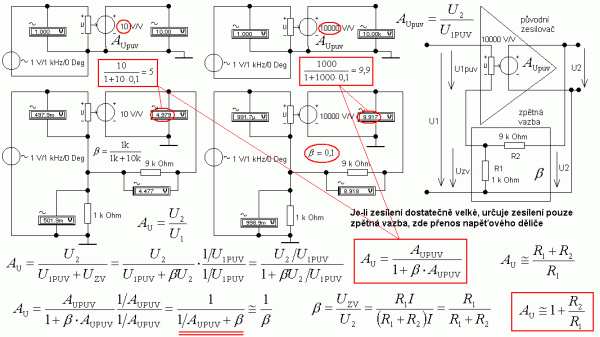
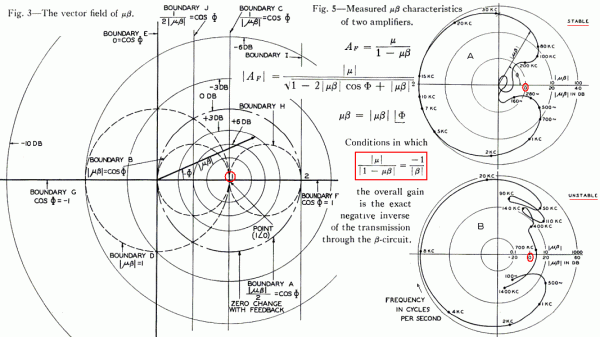
Obr. 7: Odvození přenosu zesilovače po zavedení zpětné vazby – Blackův vztah
Odvození podle schématu vpravo nahoře i simulace ukazuje, že ve jmenovateli Blackova vztahu oproti obr. 1 je plus a ne mínus, což je logické, protože záporná zpětná vazba zesílení zmenšuje a jmenovatel se proto musí zvětšovat. Ale obecně jsou jak přenos zpětné vazby, tak původní zesílení před zavedením zpětné vazby komplexní veličiny a mají tudíž znaménko, takže součin může být záporný a pak to vyjde, takže je to věc dohody. Výsledný vztah ať s plus či mínus ve jmenovateli je ve zcela nevhodném tvaru, protože při nejčastěji uvažovaném případu, kdy zesílení je extrémně velké, vede pro tuto limitu vzorec na neurčitý výraz nekonečno/nekonečno. Proto je vhodné tvar vzorce upravit (dole podtrženo). Pak je po dosazení vidět, že při velkém zesílení určuje vlastnosti zapojení opravdu pouze zpětná vazba a tou je v tomto případě přenos odporového děliče napětí (0,1). V simulaci je vidět, že už od původního zesílení 1 000 se zesílení nového zesilovače se zpětnou vazbou opravdu blíží převrácené hodnotě přenosu zpětné vazby (10). Součin přenosu zpětné vazby a původního zesílení se používá pro vyšetření stability systému. Pokud je při nějakém kmitočtu roven jedné, tak při kladné vazbě bude ve jmenovateli vztahu nula a systém se rozkmitá. Tato podmínka se nazývá oscilační a u generátorů se na rozdíl od zesilovačů o její dosažení naopak snažíme. Kdežto u zesilovačů křivka součinu v komplexní rovině nesmí reálnou jedničku obejít zvenku při žádném kmitočtu.
Obr. 8: Nyquistovo kritérium stability zesilovače se zpětnou vazbou [5]
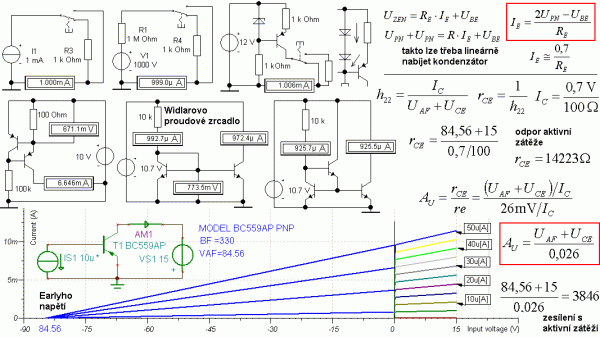
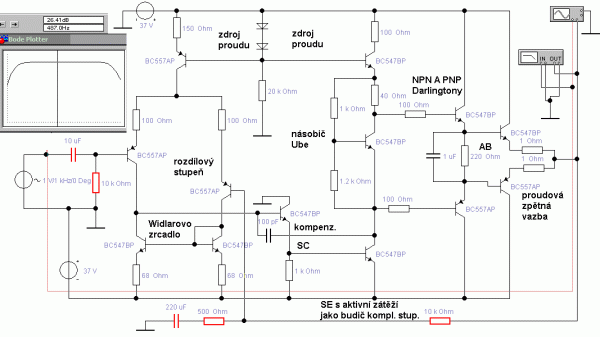
Ve vztahu pro zesílení zesilovače bývá poměr odporů a proudový zdroj má odpor velmi velký. Takže, kdyby se například kolektorový odpor nahradil zdrojem proudu, získáme zesilovač s extrémně velkým zesílením. Toto řešení se někdy označuje jako tzv. aktivní zátěž. Proudový zdroj neexistuje, ale lze se mu přiblížit. První dvě zapojení na následujícím obrázku porovnávají ideální a reálný zdroj proudu. Jako reálný zdroj proudu se chová zdroj, jehož vnitřní odpor je mnohem větší než odpor spotřebiče, takže jeho odpor už téměř nemá vliv na proud obvodem. Poslední zapojení je stabilizátor proudu s tranzistorem. Na vstupu je konstantní napětí stabilizační diody a napětí přechodu UBE se také příliš nemění, takže i na odporu bude konstantní napětí a bude jím protékat konstantní proud. Stabilizaci podpoří záporná zpětná vazba. Pokud by proud měl tendenci klesnout, zvětší se napětí na přechodu a tranzistor se více otevře a tím vykompenzuje pokles. Místo zenerky se používají dvě diody v sérii. Na spodní části obrázku je jiná varianta proudového zdroje, pro který platí stejný vztah. Proud určený Ohmovým zákonem pak protéká i spodním tranzistorem do spotřebiče (zde ampérmetru). U integrovaných zesilovačů se často používá Widlarovo proudové zrcadlo. Levý tranzistor je zapojen jako dioda, oba tranzistory pak mají stejná napětí UBE a potečou jimi tedy stejné emitorové proudy. Levý tranzistor má větší proud kolektorem o dva proudy do báze. Rozdíl mezi kolektorovými proudy lze zmenšit dalším tranzistorem, který dodá proudy do bází. Takže levý kolektorový proud bude teď jen nepatrně větší o bázový proud pomocného tranzistoru. Proud určuje napětí na odporu a to je ve druhém případě menší o 2UBE než napětí zdroje.
Obr. 9: Proudové zdroje a odvození zesílení SE s aktivní zátěží (proudovým zdrojem)
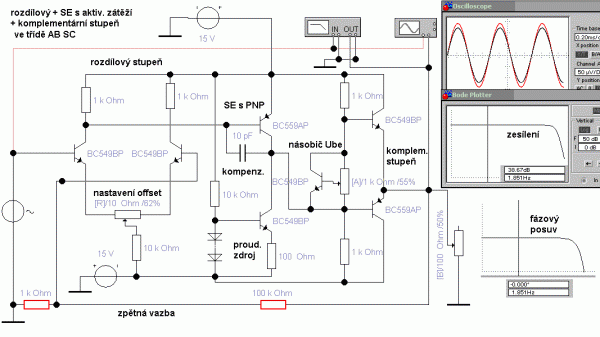
Pokud se použije místo kolektorového odporu proudový zdroj, je zapotřebí pro určení zesílení znát vnitřní odpor tranzistoru a nelze jej proto zjednodušeně položit nekonečnu. Odpor je vlastně převrácená výstupní vodivost tranzistoru h22 a ta se dá odvodit pomocí trojúhelníku s Earlyho napětím UAF, které se pohybuje mezi padesáti až dvěma sty volty. Po dosazení na základě trojúhelníku je výsledný vzorec pro zesílení stupně s aktivní zátěží docela jednoduchý, protože kolektorové proudy se ve vztahu pro zesílení při odvozování pokrátí. V simulaci v programu EWB jsou odsimulovány jednotlivé stupně zesilovače zvlášť a uprostřed je pak výsledek pro kompletní zapojení. Přepnutím osciloskopu do režimu A/B lze zobrazit i převodní charakteristiku zesilovače. Po propojení obou stupňů se zesílení vstupního rozdílového zesilovače zmenší, protože vstupní odpor budiče PNP SE komplementárního stupně je poměrně malý a je klasicky v náhradním schématu metody beta bariéry paralelně ke kolektorovému odporu. Korekce výpočtu zesílení na tuto paralelní kombinaci je pak na obrázku vpravo dole. Shoda výpočtu se simulací je velmi dobrá.
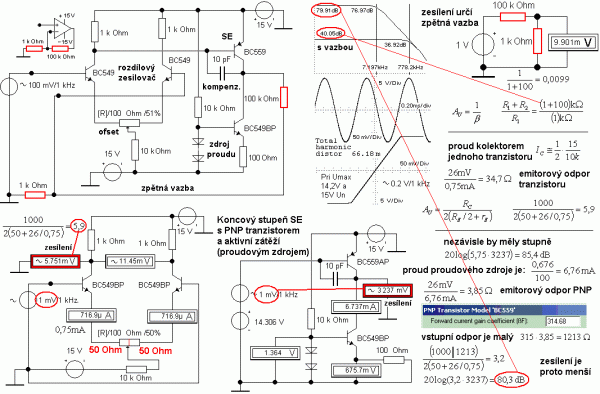
Obr. 10: Zapojení operačního zesilovače s rozdílovým stupněm a napěťovým stupněm SE
V zapojení druhého stupně je použita frekvenční kompenzace Millerovou kapacitou. Ta je u tranzistoru v parazitní formě na závěrně polarizovaném přechodu kolektor-báze přítomna vždy (viz varikap) a tato kapacita pak při vysokých kmitočtech zkratuje přechod kolektor-báze a tím propojuje výstup se vstupem. Jejím externím zvětšením lze mezní kmitočet tranzistoru ještě snížit. Na první pohled nedává taková degradace vlastností zesilovače smysl. Jenže zapojení OZ se zpravidla skládá ze tří stupňů a v každém stupni bude Millerova kapacita. Pokud se to nevhodně nakombinuje a mezní kmitočty budou následovat za sebou postupně, bude mít frekvenční přenosová charakteristika několik lomů. A s každými 20 dB na dekádu je spjatý i fázový posuv až o devadesát stupňů. To má za následek, že původně záporná zpětná vazba se díky fázovým posuvům může přetočit ve vazbu kladnou a zapojení bude nestabilní. Tomu přidaný Millerův kondenzátor v napěťovém stupni zabrání, protože charakteristika pak bude mít jen jeden lom při nižším kmitočtu. Dokonce některé typy operačních zesilovačů mají možnost zapojit tento kompenzační kondenzátor externě.
Obr. 11: Nápověda programu EWB s vysvětlením modelu OZ s frekvenční kompenzací
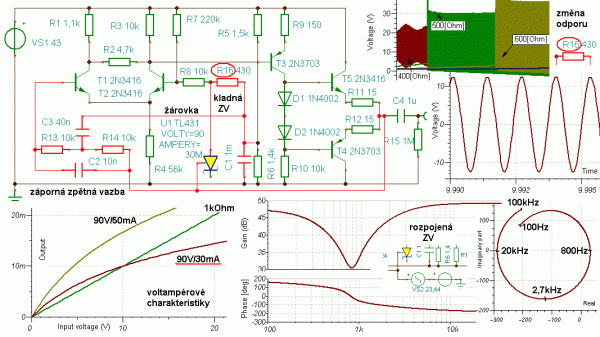
Zapojení operačního zesilovače, které je zatím poskládané z rozdílového vstupního zesilovače a napěťového stupně SE s aktivní zátěží, ještě chybí koncový stupeň. Zpravidla se použije klasické komplementární zapojení společný kolektor (SC). To pak zajistí malou výstupní impedanci zesilovače. Aby se minimalizovalo zkreslení, použije se kompromisní třída AB. Buď budou mezi bázemi NPN a PNP tranzistoru posouvací diody (obr. 14), nebo se použije sofistikovanější řešení s přesným nastavením předpětí násobičem napětí UBE.
Obr. 12: Simulace jednoduchého třístupňového operačního zesilovače
Násobič UBE má napětí PN přechodu na spodní části odporového trimru a na horní části děliče bude pak adekvátní část (stejný proud), která se přičte k tomuto napětí UBE. Trimrem lze takto nastavit pootevření koncových tranzistorů přesně a minimalizovat tak přechodové zkreslení. Toto postupně vytvořené zapojení je sice pěkné a názorné, ale je příliš citlivé na nastavení nuly (offset). Ale se stejnosměrným posuvem může být problém i u dokonalejších řešení. U přesných operačních zesilovačů bývá dokonce možnost připojení trimru pro nastavení stejnosměrného offsetu. Takže existují i integrované operační zesilovače s více vývody pro nastavení offsetu a frekvenční kompenzace. Často se staví i nízkofrekvenční výkonové zesilovače se strukturou operačních zesilovačů. Na internetu jsem kdysi našel docela pěkné zapojení, bohužel dnes už si nepamatuji zdroj. V překresleném zapojení do programu EWB nebyly použity výkonové tranzistory. Na vstupu i ve zpětné vazbě jsou zařazeny kondenzátory, takže zesilovač nebude zesilovat stejnosměrné signály a bude omezen na NF rozsah. Derivační článek na vstupu určuje i vstupní odpor zesilovače (10 k).
Obr. 13: Nízkofrekvenční výkonový zesilovač se strukturou operačního zesilovače
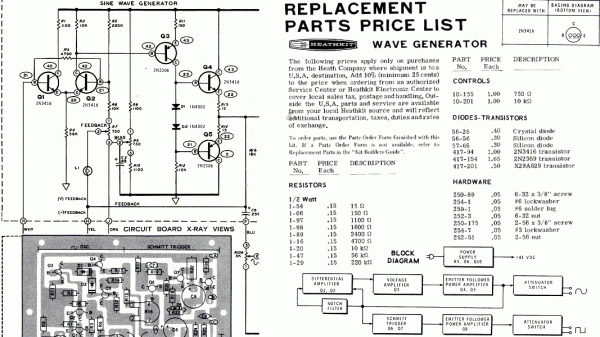
Zesilovač RC generátoru Heathkit IG-18 je minimalistická verze zesilovače se strukturou operačního zesilovače. Bohužel nikde jsem nenašel kompletní manuál, takže následující obrázek je složen z několika částí. Tranzistory a i zapojení se v různých verzích generátoru liší [10].
Obr. 14: Zesilovač audio generátoru Heathkit verze IG-5218 [10]
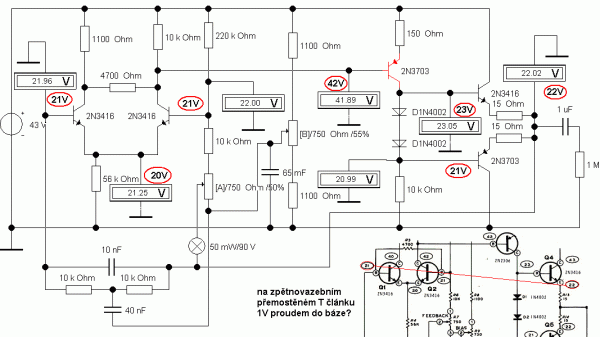
K žádné z verzí použitých PNP tranzistorů není k dispozici SPICE model. Obvod ale není citlivý na přesnou volbu tranzistoru, takže pracovní body jsou nastaveny velmi přesně na první pokus jen nepatrnou změnu potenciometru B. Program EWB má velmi pěkně vyřešenu multimediální simulaci, kdy se jezdec potenciometru posouvá pomocí předvolené klávesy (B a Shift B) a přístroje v zapojení okamžitě reagují. Ve zpětnovazebním T článku budou pravděpodobně větší odpory, protože pokud není v manuálu chyba, měl by na nich být úbytek napětí jeden volt.
Obr. 15: Kontrola pracovních bodů multimediální stejnosměrnou simulací DC
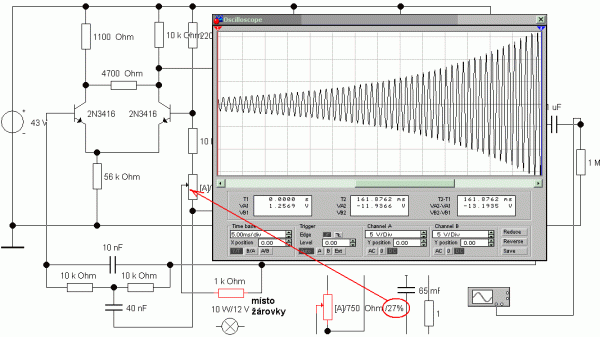
Simulace kmitavých obvodů je obecně obtížná a toto zapojení je na hranici možnosti programu EWB. Ale rozkmitat to nakonec jde, jen se nesmí v základním nastavení podmínek transient analýzy nic měnit. Dále bylo nutné nahradit EWB žárovku odporem a kmity jsou bez automatické regulace, takže jsou netlumené až do limitace napájecím napětím.
Obr. 16: Rozkmitání generátoru po spuštění multimediálního módu simulace
U programu Tina je možné pro nastavení pracovního bodu použít optimalizační analýzu. Zvolí se u potenciometru jako parametr procenta nastavení jezdce a pak DC Goal function v optimalizační analýze určí nastavení potenciometru pro požádované stejnosměrné napětí pro připojený voltmetr. Pro zpřehlednění zapojení byly nakonec potenciometry nahrazeny pevnými odpory. Na rozdíl od programu EWB, kde se to rozkmitalo při volbě výpočtu pracovních bodů, je u programu Tina potřeba naopak nastavit nulové počáteční podmínky analýzy transient. Do modelu žárovky bylo podle [11] zadáno 90 V / 30 mA. Program má se simulací zapojení problémy a dlouho trvá, než výpočet nakonec proběhne. Místo nastavení potenciometru byl R16 měněn krokováním, aby se zjistilo, kdy poklesne amplituda kmitů z limitace a oscilátor se ještě rozkmitá.
Obr. 17: Rozkmitání generátoru s nelineární žárovkou 90 V / 30 mA v programu Tina-TI9
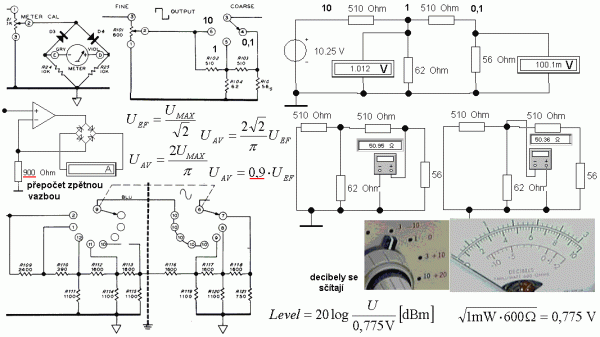
Na výstupu generátoru je dělič úrovně (attenuator) poskládaný tak, aby se neměnil výstupní odpor, což je zkontrolováno na jednodušší části pro obdélníkový výstup. Rozsahy sinusového průběhu jsou voleny tak, aby bylo možné snadno měřit i s decibelovými úrovněmi dBm (miliwatt na 600 ohmech). Stupnice voltmetru je cejchována v efektivních hodnotách, ale měřidlo měří hodnotu střední. Kdyby se provedla náhrada elektronickým voltmetrem s operačním zesilovačem dle obrázku vlevo, je zapotřebí upravit pro správný přepočet zpětnou vazbu, což je jednodušší než překreslení stupnice.
Obr. 18: Kontrola útlumového článku a měřič úrovně generátoru Heathkit IG-18
Tímto bych zakončil poněkud široce pojatý seriál věnovaný simulaci generátoru firmy Heathkit, který mi posloužil jako příklad opravdu povedené konstrukce, která má navíc potenciál dalšího podstatného zdokonalení [12]. Je opravdu škoda, že tato firma před pár lety pravděpodobně definitivně zanikla. Společnost původně vyráběla letadla, ale nejslavnější je období, kdy produkovala dokonalé stavebnice pro bastlíře. S rostoucí miniaturizací a razantním zlevněním spotřební elektroniky přišel asi logický konec a firmu nezachránily ani projekty pro školství a vzdělávání. Pokud jsem to pochopil správně, tak aktuální stav je asi takový, že nějaká právnická firma skoupila duševní vlastnictví. Ale na wikipedii [13] jsou mírně optimističtí a naznačují, že by mohlo dojít k obnovení firmy. Každopádně když zadáte do libovolného internetového vyhledávače heslo Heathkit, tak vypadne neuvěřitelné množství odkazů. Podle mne to byla naprosto úžasná firma.
Obr. 19: Analogový počítač na skládání harmonických (Fourier synthesizer) [9]
Obr. 20: Součástky a propojovací (nezničitelné) vodiče k analogovému počítači MEDA
Obr. 21: Vysokonapěťový dělič napětí k voltmetru (1 500 000 000 Ohmů)
Obr. 22: Regulační odpory a děliče napětí
Neon Tube Generator (High Voltage oscillator a návrh kapacity zdroje)
Singing AM transformer (Shockley equation PN junction, SPICE model diody)
Download a odkazy: