Odstředivé vychýlení koulí je převedeno na svislý pohyb nožového mechanismu, který nakonec táhlem ovládá vstup - ventil přívodu páry, anebo u modernějších strojů přímo přívod paliva (plyn). Je to příklad dokonalé záporné vazby, která stabilizuje výstup - otáčky stroje se setrvačností danou hmotností soustavy. Naprosto shodnou funkci při stabilizaci amplitudy výstupu generátoru, tj. jeho kmitů, plní žárovka s tepelnou setrvačností vlákna. Tato funkce žárovky (incandescent lamp) je označována jako Automatic Level Control (ALC), anebo Automatic Gain Control (AGC). V grafech průběhů by výšce závaží (otevření ventilu) odpovídala teplota vlákna žárovky.
Žárovka je vynikajícím regulačním prvkem a podle [1] se bez problémů v žárovkou stabilizovaných zapojeních dosahuje harmonického zkreslení menší než setina procenta a existují i konstrukce s 0,0005 % THD (total harmonic distrotion). Setrvačnost vlákna je přitom velkou výhodu. Lze to přirovnat ke světlu žárovky při střídavém napájení-vlákno při průchodu nulou nestihne vychladnout a svit (u generátoru odpor) se mění minimálně. Stejnou funkci jako žárovka zastane i polovodičový termistor PTC. VA charakteristice žárovky se podobá v oblasti kolena i výstupní charakteristika tranzistoru. V řadě zapojení je proto použit JFET a při správném návrhu vazby lze dosáhnout až 0,00002 % THD. Pokud se nelineární prvek umístí na opačnou stranu zpětné vazby, lze použít NTC termistor anebo antiparalelně zapojené diody s odpory, které dotvarují charakteristiku inverzně k žárovce. Místo tepelně setrvačného děje lze využít i pomalou reakci fotoodporu a vyrobit si ve smršťovací bužírce optický vazební člen se zelenou LED a CDS fotoodporem. Žárovka má ale umístěním vlákna do skleněné baňky výraznou výhodu oproti ostatním řešením a tou je izolace od vlivu okolí. Žárovka je tou správnou volbou pro nejjednodušší realizaci AGC s výbornými parametry.
Obr. 1: Oscilátor s posouvanou fází (Phase-shift oscillator)
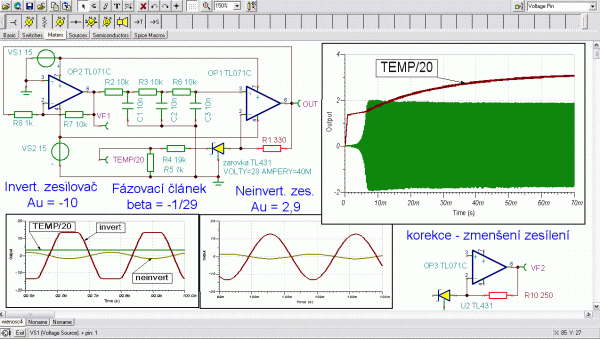
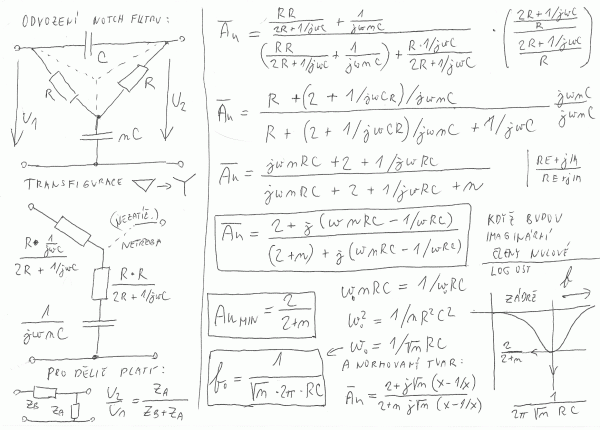
Pokud má oscilátor ustáleně kmitat, nesmí se měnit po rozkmitání výstupní, ale samozřejmě ani vstupní napětí. Tj. kolikrát zesilovač napětí zesílí, tolikrát ho musí zpětná vazba zpět zeslabit. Pokud je zesilovač invertující, musí o 180 stupňů, tedy do protifáze, posunout signál samozřejmě i zpětná vazba. Tento ustálený stav se označuje jako oscilační podmínka. K posuvu fáze lze použít například tři integrační nebo derivační články a posuv se mezi ně rozdělí po 60 stupních, pokud budou mít stejnou časovou konstantu RC. Jsou-li články stejné, je výsledný přenos jen -1/29 a k odvození přenosu soustavy článků je zapotřebí používat postupně transfiguraci trojúhelník-hvězda s komplexními impedancemi. Postup odvození je naznačen na obr. 5. Varianta zapojení označovaná jako Buffered phase-shift oscillator má jednotlivé RC články oddělené opakovacími neinvertujicími zesilovači. Pak se jednotlivé RC články vzájemně nezatěžují. Z fázorového diagramu sériového RC spojení lze odvodit, že přenos článku je kosinus fázového posuvu, protože úhlopříčkou diagramu je vstupní napětí a strana obdélníku je napětí výstupní. Kosinus 60 stupňů je 1/2 a články jsou tři za sebou, takže výsledný přenos článku je pak -1/8. Pro splnění oscilační podmínky pak musí invertující zesilovač zesilovat osmkrát. Použijí-li se tři derivační CR články s dekadicky rostoucímí odpory a analogicky dekadicky klesajícími kapacitami, bude se zapojení blížit variantě s oddělovacími zesilovači a potřebný zisk invertujicího zesilovače bude asi desetinásobný. Z fázorového diagramu pro impedance při šedesáti stupních lze pomocí funkce tangens dořešit i podmínku pro kmitočet f = 1/(2piRCtang60). V zapojení na obr. 1 byl ponechán třikrát zesilující AGC zesilovač z předchozího oscilátoru s Wienovým článkem a zesílení bylo dorovnáno invertujicím zesilovačem na oscilační podmínku. SPICE model žárovky byl otočen vzhůru nohama, aby se ověřila správnost modelu vůči uzlům země.
Obr. 2: Porovnání zkreslení signálu Phase-shift oscilátoru s a bez AGC [2]
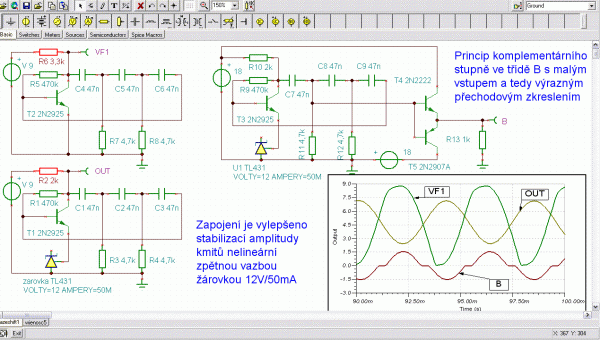
Zapojení s posouvanou fází je nepraktický obvod vhodný spíš pro vysvětlení oscilační podmínky než pro praktické použití. Jedinou jeho výhodou je, že ho lze sestavit i s jedním tranzistorem v invertujicím zapojení se společným emitorem (SE). Filtr třetího řádu vyžaduje při ladění současně měnit synchronně tři prvky a zapojení se proto používá jen na generátory s pevně nastaveným kmitočtem. Simulace jednotranzistorového zapojení se ukázala jako značně obtížná. Osvědčila se až varianta SE se zpětnovazebním nastavením pracovního bodu podle [2]. Chybějícím odporem posledního derivačního článku je vstupní odpor zesilovače SE. Vstupní odpor SE je bez zpětné vazby malý a ve většině uveřejněných schémat je to opomenuto. Takto zjednodušená zapojení zpravidla kmitat nebudou, protože vstupní odpor tranzistoru prakticky vyzkratuje poslední prvek fázovacího článku. Snaha zvednout hodnotu vstupního odporu SE zapojení proudovou zpětnou vazbou je kontraproduktivní, protože vazba zároveň snižuje potřebné zesílení. V zapojení s OZ na obr. 1 tento problém odpadá, protože neinvertujicí zapojení má odpor velmi velký. Všimněte si i dokonalé filtrace, která ze signálu v limitaci v levé části neupraveného zapojení na obr. 2 vybírá jen tu správnou sinusovou nezkreslenou složku a opravuje tak tvar signálu. Filtrací lze principiálně získat sinusovku i z obdélníku odfiltrováním vyšších harmonických. Problém malého vstupního odporu lze obejít použitím unipolárního tranzistoru, ale po pravdě ani tak se mi simulace nedařila. Jednotranzistorové zapojení ale dobře demonstruje blahodárné účinky žárovky (AGC) na kvalitu (THD) výstupního signálu. Protože na obr. 2 zbylo ještě místo, je tam naznačen i výstupní komplementární stupeň v zapojení emitorový sledovač v čisté třídě B s malým vstupním signálem a proto i velmi výrazným přechodovým zkreslením. V reálném generátoru na obr. 3 jsou proto mezi bázemi komplementárních tranzistorů posouvací diody - třída AB.
Simulace je jen simulace a nepostihuje samozřejmě úplně všechny reálné situace. Jednou velmi nepříjemnou skutečností je, že SPICE algoritmy špatně realizují funkci kondenzátoru jako akumulátoru elektrické energie do výstupu při nesymetrickém napájení zesilovače. Model žárovky byl v zapojení otočen zpět trojúhelníkem k zemi, protože algoritmům to vyhovuje lépe. Dalším opomíjeným problémem může být i maximální velikost proudu, který lze v reálném zapojení vytáhnout z výstupu operačního zesilovače. Proud zpravidla nepřekračuje miliampéru. S tím samozřejmě souvisí volba typu žárovky. Podrobně se této problematice věnují stránky [1]. Odpor vlákna musí být při použití operačních zesilovačů velký. To vede podle Ohmova zákona na žárovky pro malé proudy a velká napětí. V původních konstrukcích jsou to desítky miliampér a desítky voltů (např. v oscilátoru IG18 90 V / 30 mA). Žárovky podobných hodnot se používaly například v telefonních ústřednách a v nouzi je samozřejmě možné žárovky na nižší napětí řadit sériově. Ale i dnes se dají i u nás koupit signální žárovky 130 V / 20 mA v patici E10. Navíc je to ještě mnohem nepříznivější, než to na první pohled vypadá. V dále zvoleném zapojení Notch-filter generátoru bude žárovka na opačném místě zpětné vazby a zesílení je relativně velké, což vede na požadavek značně velkého odporu žárovky.
Další otázkou je, jak zvolit pracovní bod žárovky. Měl by být na křivějším počátku VA charakteristiky, ale přitom dostatečně daleko, aby vlákno bylo dostatečně horké a nereagovalo tak na teplotu okolí. Doporučení se v pramenech různí, ale pohybuje se to mezi 1/20 až 1/10 jmenovitého napětí žárovky. Vzhledem k linearizaci našeho SPICE modelu odporem 20 ohmů v počátku bude asi vhodnější pro simulaci spíše vyšší hodnota napětí pracovního bodu. Jednoduchou online kontrolu při návrhu dává teplotní tykadlo modelu žárovky (většinou to v simulacích vychází mezi stem až dvěma sty stupni). Protože je to jen simulace a navržený model žárovky umožňuje jednoduše v dialogovém okně nastavit libovolné parametry žárovky, lze si při simulování a oživování modelu zapojení pomoci naprosto libovolnou žárovkou. Případně lze zasáhnutím do netlistu (enter macro) změnit i teplotní setrvačnost vlákna (tau kondenzátor) či dokonce i překmit (číslo 9 v rovnici zdroje).
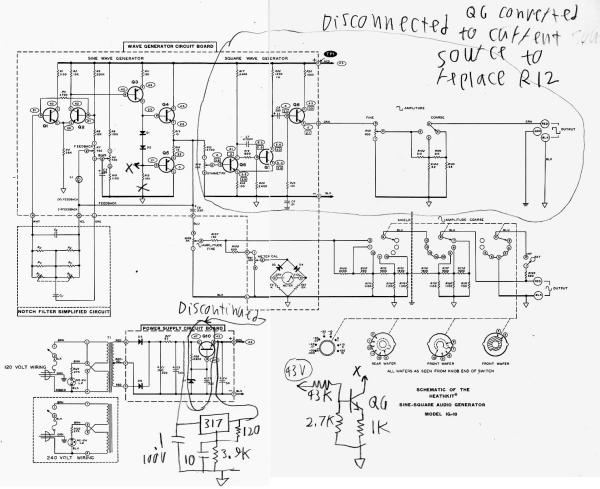
Obr. 3: Heathkit IG18 z roku 1969 - nadčasové a geniální řešení nf RC generátoru [4]
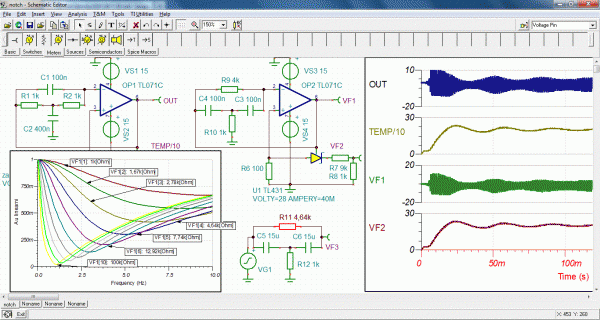
Po vyřešení problému automatické stabilizace amplitudy kmitů AGC volbou teploty nažhaveného wolframu v inertní atmosféře ve skleněné baňce už jen zbývá zvolit správné zapojení generátoru. Za dokonalé jsem vždy považoval řešení W. Hewletta uvedené v předchozím článku. Ale na internetu objevená Heathkit IG18 konstrukce [4] mi přijde ještě lepší. Pět tranzistorů vlevo nahoře tvoří jednoduchý operační zesilovač. Pro stabilizaci je samozřejmě použita žárovka, ale princip je otočený. Místo pásmové propusti v kladné zpětné vazbě vybírá kmitočet pásmová zádrž (Notch filter) ve vazbě záporné. Zvolené zapojení přemostěného T článku přitom zachovává možnost ladění tandemovým potenciometrem. Volba poměru kapacit mostu n = Cpillar/Cbridge skýtá možnost dotvarování přenosové a fázové charakteristiky se zachováním jednoduchého přepínání kmitočtových dekád rozsahů.
Mimochodem označení laditelného generátoru s pásmovou propustí jako Wien-bridge oscillator je nesmyslné a W. Hewlett má dokonce v grafu v patentové přihlášce chybně vykreslenou fázovou charakteristiku. Prvky Wienova článku v kladné vazbě lze přeskládat jak sirkový hlavolam dvěma dalšími způsoby bez nejmenšího vlivu na chování obvodu. Podobnost s Wienovým mostem je i přes skutečnost, že při rozkmitání je zapojení v úhlopříčce mostu vyvážené, nepodstatná. Důležité je jen splnění oscilační podmínky a skutečnost, že pásmová propust zajistí tuto podmínku jen pro jeden kmitočet. Kdyby tomu tak nebylo, nebyly by kmity harmonické (sinus). Navíc pokud se člověk zamyslí, tak rozhodující je zde fázová charakteristika, která prolítává nulou pod dostatečným sklonem, kdežto amplitudová charakteristika má tvar hory Říp s neostrým maximem. Z tohoto pohledu jsou na tom lépe LC oscilátory s rezonančními obvody. Ale díky odmocnině v Thomsonově vztahu pro rezonanční kmitočet mají v principu velmi malou přeladitelnost. Navíc malé hodnoty kapacit lze v RC generátorech snadno vykompenzovat velkými hodnotami odporů, což u LC oscilátorů nejde, protože MegaHenry na rozdíl od MegaOhmů neexistují. Heathkit IG18 má úžasně vyřešeno i nastavování kmitočtu podobně, jako když se na klasické odporové dekádě volí odpor a tento nf audiogenerátor z roku 1969 prodávaný jako stavebnice kmitá už od 1 Hz. Obě koncepce ale za své dokonalé vlastnosti vděčí žárovce, tedy dokonalému vyřešení AGC. Takže spíše než Wien by si toto zapojení zasloužil pojmenovat po sobě pan James Watt, který problém stabilizace zápornou zpětnou vazbou vyřešil jako první.
Obr. 4: Odvození přenosu zádrže Hall nework laditelné jedním prvkem 1979 [3]
Ladění kvalitní pásmové zádrže lze realizovat i jediným ladicím prvkem – obyčejným potenciometrem. Filtr Hall network [3] má bohužel malou přeladitelnost, respektive na krajích zvoleného pásma se výrazně zmenšuje dosahovaný maximální útlum a s tím už si jednoduchý AGC obvod se žárovkou neporadí a muselo by se to řešit elektronickým stejnosměrným servem. A takováto komplikace zapojení za vypuštění tandemového potenciometru nestojí. Profesionálně vyráběné generátory dávaly přednost duálním ladicím kondenzátorům, protože bylo snadnější zajistit souběh obou prvků. Takže volba koncepce je jasná. Ladění tří prvků je obtížně proveditelný nesmysl a jedním prvkem laditelný RC filtr má zase problémy se závislostí velikosti útlumu na naladěném kmitočtu. Zbývá tedy buď dvěma prvky laditelná pásmová propust v zapojení W. Hewletta, anebo pásmová zádrž zapojení oscilátoru IG18. Čmáranina Hall network je půvabná. Pokud nad ní hodláte bádat, tak je v ní použit místo komplexního kmitočtu (j omega) operátor p = 2*pi*f , který se ale oproti našim zvyklostem značí písmenkem malé s.
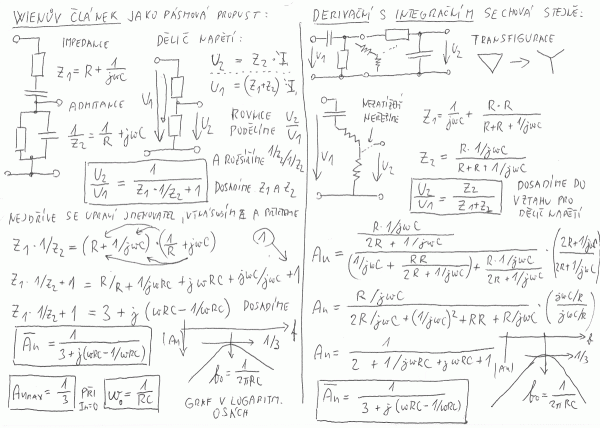
Obr. 5: Odvození Wienova článku a důkaz pro jinou konfiguraci prvků pásmové propusti
Wienův článek bývává odvozován zbytečně složitě. Pokud se hned na začátku upraví elementární vzorec pro přenos děliče s vědomím, že na výstupu je paralelní kombinace prvků, lze výsledku dosáhnout prakticky okamžitě. S odvozením kaskádního spojení horní a dolní propusti už je to horší. Nejrychleji asi vede k výsledku transfigurace trojúhelník-hvězda s tím, že poslední impedanci není zapotřebí přepočítávat, protože dělič je nezatížený a tím pádem impedancí nebude protékat proud a na chování obvodu se tato impedance neprojeví. Stejným způsobem by šlo odvodit zapojení s posouvanou fází. Sirkový hlavolam zpětné vazby lze přeskládat ještě jedním způsobem a to tak, že nejdříve bude zapojen článek integrační a teprve za ním derivační. Všechna tři zapojení jsou vzájemně zaměnitelná a z tohoto důvodu je tedy označení Wien-bridge oscillator opravdu nesmyslné. Rozborem komplexního vztahu pro výsledný přenos se odvodí, že maximum propusti je 1/3 pro omegu rovnou převrácené časové konstantě RC. Kdyby se slušně chovaly i reálné indukčnosti a při simulaci samozřejmě budou, šly by poskládat další tři varianty propustí s cívkami.
Obr. 6: Odvození přenosu pásmové zádrže přemostěného T článku (Bridged-T notch filter)
U přemostěného T článku se asi bez transfigurace obejít nedá, ten trojúhelník k přepočtu na hvězdu přímo vybízí. Pokud budou ve výsledném vztahu imaginární závorky rovny nule, vypadne tvar pro minimální přenos. Ze vzorce pro kmitočet vyplývá, ze s rostoucím útlumem (poměrem kapacit) se kmitočet posouvá směrem k nižším kmitočtům. Protože existuje i duální zapojení s prohozenými odpory a kondenzátory, mohl by být na místě pilíře mostu nebo přemostění potenciometr a změnou velikosti jeho odporu by bylo možné filtr ladit stejně jednoduše jako u Hallova zapojení jedním prvkem. Ale má to stejný problém, protože se změnou naladění se mění minimální přenos. Muselo by se pak vyřešit automatické elektronické navyšování zisku zesilovače ve velkém rozsahu. Ve vzorci pro kmitočet je odmocnina z n, takže v případě typického desetinásobného přeladění by vycházela těměř stonásobná změna přenosu článku a tedy i zisku zesilovače, aby byla splněna oscilační podmínka. Je sice příznivé, že potřeba většího zisku je na nižších kmitočtech, ale realizace tohoto principu by asi rozhodně nebyla jednoduchá.
Byla vynechána možnost nesymetrického Wienova mostu s n poměrem prvků. Protože se ale v principu jedná o zapojení horní a dolní propusti, lze si chování snadno přestavit, když přenosové charakteristiky CR a RC budeme posouvat proti sobě na kmitočtové ose. Když budou charakteristiky blíž k sobě, tak výsledná bude mít stejný tvar, ale protne se to při mnohem nižší hodnotě přenosu. Naopak když budou mezní kmitočty horní a dolní propusti daleko od sebe, bude výsledná přenosová charakteristika připomínat charakteristiku reproduktorové výhybky pro střední reproduktor. Přenos sice vystoupá až k jedničce, ale přestane to fungovat jako selektivní obvod. Proto u Wienova článku nemá smysl použít jiné, než shodné prvky. U přemostěného T článku lze asi vést diskusi nad poměrem prvků (obr. 7) a hledat optimum, anebo po vzoru IG18 generátoru vzít nejjednodušší volbu pro nákup součástek-jistotu desetinásobku. Pak bude maximální útlum zádrže na jedné šestině. Krokování poměru n = R11/R12 a jeho vlivu na tvar přenosové charakteristiky s lineárními osami je na obr. 7 naznačen. Byla provedena opakovaná AC analýza s krokováním poměru v rozsahu 1 až 100 v deseti krocích s logaritmickou volbou kroku simulace.
Obr. 7: Oscilátory s přemostěnými T články a vliv poměru n na přenosovou charakteristiku
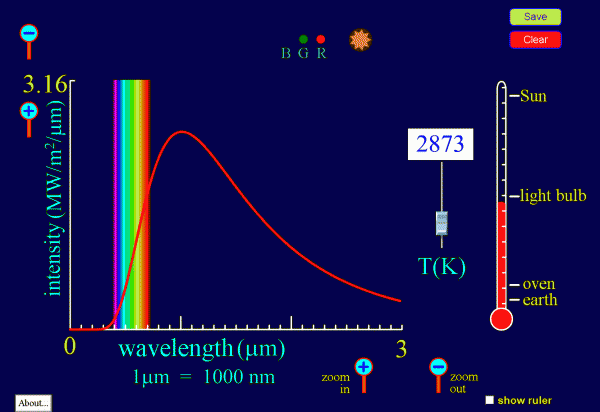
Na závěr ódy na žárovku a její použití ve zpětné vazbě ještě trochu fyziky [5]. Stejně, jako není záhada, co se stane s vodou při mínus dvaceti, není záhadou, že v americké hasičárně svítí edisonka už 110 let. Uhlíková žárovka má masivní plný profil vlákna oproti dnešním wolframovým, žárovkám, které mají tenký wolframový drátek smotaný do dvojité šroubovice. Velkou výhodou je i opačná teplotní závislost uhlíku, takže se při zapnutí nekoná proudový náraz. Ale hlavně ta uhlíková žárovka, která ani při jmenovitém napětí téměř nesvítí, jen žhne, nebude provozována jako svítidlo, ale jako podžhavená atrakce. A životnost žárovky je mocninou funkcí s dvanáctou mocninou vzhledem k nominální hodnotě. Pokud se žárovka dostatečně podžhaví, její životnost se bude blížit nekonečnu. Co by se tak asi teplému vláknu umístěnému ve vakuu či inertním plynu zatavenému ve skleněné baňce mohlo stát? Věčné světlo lze snadno vyrobit i doma. Stačí upravit svítidlo tak, aby se stejné žárovky zapojily do série a takhle vyrobená bludička bude svítit i vašim vnoučatům. Má to jen jeden drobný problém, který je názorně vysvětlen v [6] hned na prvním grafu. Závislost se jmenuje Wienův posun. Podžhavením se skoro celé spektrum posune do tepelné oblasti. A takto vyrobený zdroj spíš připomíná přetopená kamna než svítidlo.Omezená životnost 1 000 hodin u žárovek proto není žádná konspirace, ale jen zvolený kompromis mezi životností a alespoň trochu rozumnou účinností světelného zdroje [8]. Trochu vylepšit to už jde jen halogenidovým cyklem v halogenkách.
A i přes tažení EU proti neúsporným světelným zdrojům lze i dnes bez problému zakoupit 100 W žárovku a to dokonce s větší životností než mají úsporky (8 000 hodin). Používají se v semaforech na křižovatkách, protože režie spojená s výměnou za trochu ušetřené energie rozhodně nestojí. A podžhavené žárovky se prodávaly vždycky, komicky označené jako něco extra s prodlouženou životností a taktně zamlčené, že téměř nesvítící. A dodnes neexistuje světelný zdroj, který by se parametry (náběh do plného jasu, stroboskopický jev, směrová charakteristika) a kvalitou světla (index barevné věrnosti RA) žárovce vyrovnal. Nejblíže tomu asi mají podsvětlovací trubice LCD displejů a LED diody monitorů. Obojí se dnes už prodává i v Edisonově žárovkové patici. Bohužel mizerná účinnost žárovky (5 % wolfram, 0,5 % uhlík) je dána fyzikálními zákony vyzařování absolutně černého tělesa a nejde to nijak obejít [8]. Otázkou ale je, zda to až tak moc vadí, protože platí i zákon zachování energie a to teplo se nikam neztratí a zůstane v místnosti a zpravidla se stejně nejvíce svítí v zimě. A i u těch semaforů může být odpadní teplo ve sněhové vánici výhodou. Každopádně o žárovku použitou ve zpětné vazbě generátoru se není třeba bát. Je podžhavená na desetině jmenovitého napětí a konstrukci generátoru určitě přežije.
Obr. 8: Livermore, bulb was installed in 1901 a svítí a svítí a má i vlastní webovou kameru [7]
Obr. 9: Žárovka 90 V / 30 mA na desce oscilátoru Heathkit IG18 [4]
Obr. 10: Model regulátoru otáček ve světelném mixu žárovek v místnosti a ohně
Obr. 11: Interaktivní stránka [8] se simulací spektra wolframové žárovky
Download a odkazy:
- GRAPH: http://www.padowan.dk/download/
- TinaTI: http://www.ti.com/tool/tina-ti