Mezi tyto úlohy patří určení rezonančního kmitočtu reproduktoru, případně indukčnosti kmitací cívky reproduktoru. Jako inspirace posloužil kolaps Tacoma Narrows Bridge rozkmitaný větrem do destruktivní rezonance. Mimochodem nedůvěra v média je dnes už na takové úrovni, že někteří studenti jsou ochotni se dohadovat u dodatečně kolorované verze filmu, že pád mostu je fake vyrobený v Hollywoodu. Podobných videí na variantu zrušení kroku na mostě je na YouTube celá řada. Za velmi půvabné shledávám rozkmitávání lávky přes potok na jednotlivých harmonických Boba Barretta.
Pro mechanickou rezonanci platí známý Thomsonův vztah pro rezonanční kmitočet paralelního LC rezonančního obvodu. Místo indukčnosti vystupuje ve vztahu hmotnost kmitajícího závaží na pružině a místo kapacity reciproká hodnota tuhosti pružiny (poddajnost). Tlumení se projeví jako paralelní odpor. Snahou výrobců reproduktorů je samozřejmě, aby rezonance byla pokud možno potlačena a posunuta do nejnižších kmitočtů mimo oblast použití reproduktoru. K destrukci jako u Tacoma bridge sice nedochází, ale kmitočty v oblasti rezonance budou zvýrazněny a někdy to přejde až v nepříjemné „chrastění“ reproduktoru.
Pro demonstraci rezonančního jevu je proto naopak vhodné zvolit reproduktor s výraznou rezonancí dle katalogových listů reproduktorů, které se dají dohledat na netu. Mně dobře posloužil nějaký 30 let starý „noname“ reproduktor z darovaných ruských reprobeden. V bednách byl jako tlumicí materiál použit molitan a po těch letech se tento molitan změnil v lepkavou nevábnou hmotu. Pokud se vyjde z úvahy, že při rezonanci je výchylka maximální, můžeme z reproduktoru vrhat i předměty. Samozřejmě předměty by měly být lehké, aby svou hmotností neovlivnily rezonanční kmitočet. U velkých reproduktorů jsem kdysi zkoušel vystřelovat mimo jiné i pingpongový míček.
Obr. 1: Video metání pingpongového míčku z reproduktoru při rezonanci
Zkoušený ruský reproduktor vykazoval výraznou rezonanci a metal ven ochotně libovolné předměty. Nejhezčí „taneček“ ale dělal vrut vypadlý ze skříňky. Protože je feromagnetický, tak na něj kromě gravitace působí i pole permanentního magnetu reproduktoru a stavěl se při tanci hezky na špičku.
Obr. 2: Start vrutu při rezonančním kmitočtu 67 Hz
Ještě než popíši vlastní měření, zastavím se na chvíli u Williama Thomsona. Už ve svých 22 letech byl řádným profesorem a za své vědecké zásluhy byl povýšen do šlechtického stavu. Přijal šlechtické jméno podle říčky, která protékala v blízkosti jeho laboratoře. Myslím, že tato informace, že Baron Kelvin of Largs je totožný s Williamem Thomsonem, není příliš známá. Na druhou stranu na Wikipedii také píší, že několikrát v životě prohlásil, že rádio nemá budoucnost, že předměty těžší než vzduch nebudou nikdy létat a že se co nevidět dokáže, že rentgen je jen kouzelnický trik.
Obr. 3: První pokus hledání rezonance pomocí krokodýlku (fotoaparát FUJI100S)
Rezonanční výchylka je větší než odpovídá buzení a protože se s membránou hýbe i kmitací cívka v poli permanentního magnetu reproduktoru, chová se obvod i jako generátor a v cívce se indukuje napětí. To má vliv i na průchod proudu a napětí na cívce. Existují různě komplikované náhradní modely reproduktorů s gyrátory. Když si ale člověk představí impedanční křivku reproduktoru, kde vlevo je typická paralelní rezonance a vpravo je induktivní nárůst impedance cívky, tak lze použít nejjednodušší model reálné kmitací cívky (sériové spojení odporu cívky s její indukčností) a reálný paralelní rezonanční obvod odpovídající mechanické rezonanci přepočítané na elektrickou stranu.
Pokus s rezonančním vypuzováním předmětu z reproduktoru byl úspěšný, ale přece jen je vhodnější zapojit nějaké měřidlo a určit rezonanci přesněji. Při nízkých kmitočtech lze zanedbat reaktanci kmitačky a obvod pak tvoří generátor s jeho vnitřním odporem 75 Ω v sérii s malým odporem reproduktoru 4 Ω na který je připojený jeho rezonanční obvod. Zapojení odpovídá pásmové propusti, takže při rezonanci bude na rezonančním obvodu maximální napětí. To lze indikovat třeba osciloskopem při vypnuté časové základně anebo multimetrem. Starý analogový PU500 jako indikátor rezonance je pro tento účel vhodnější, protože pohyb ručičky je názornější než měnící se číslice displeje digitálního multimetru.
Obr. 4: Rezonance snímaná kamerou s frekvencí 120 snímků/s (SONY HD-AZ1)
Vyšší snímací frekvence kamery zvýrazní pohyb membrány při rezonanci, ale zrakový vjem při pokusu odpovídá předchozímu videu z fotoaparátu. Člověk totiž větší výchylku na kmitočtu 66 Hz pouhým pohledem nerozpozná, protože oko na tak rychlé změny nereaguje dostatečně rychle. Ještě názornější je samozřejmě zpomalený záběr Slowmotion, který lze navolit přímo na kameře.
Obr. 5: Zpomalené video při ladění generátoru směrem nahoru
Multimetr Metrix MTX3283 kontroluje laděný kmitočet, aby se zobrazil v záběru videa. Má také grafické znázornění předchozích hodnot (takový pomaloběžný osciloskop), takže na jeho displeji lze rozeznat i průběh kmitočtu při předchozích ladicích pokusech.
Obr. 6: Zpomalené video při ladění generátoru směrem dolů
Pro určení všech elektrických náhradních parametrů reproduktoru je zapotřebí odměřit celou impedanční charakteristiku. Pro odměření je vhodnější zvolit generátor s menší výstupní impedancí než je 600 Ω, aby reproduktor hrál hlasitěji a režim se trochu blížil reálnému nasazení měniče. Simulační programy pro návrh reproduktorových soustav (např. LspCAD) umí pracovat i s tabulkou odměřených impedančních hodnot reproduktoru, ale pro jednodušší návrh stačí znát kromě odporu cívky alespoň její indukčnost kvůli její případné kompenzaci RC členem (Zobel network).
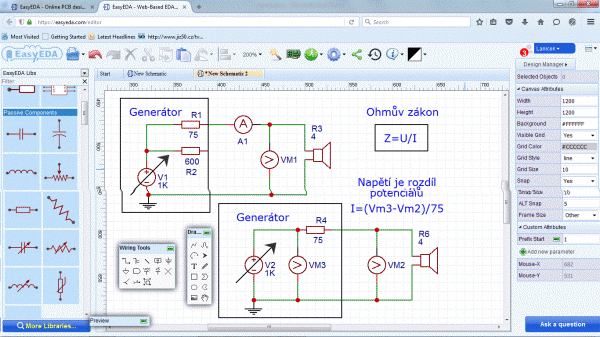
Obr. 7: Schéma zapojení měření impedanční charakteristiky reproduktoru (program EasyEda)
Jako zdroj signálu pro měření impedanční charakteristiky byl použit generátor BM 492. U tohoto generátoru je malá zrada, vnitřní voltmetr předpokládá zatížení jmenovitou impedancí, jinak vnitřní voltmetr ukazuje poloviční hodnotu napětí na výstupu bez zatížení. Na výstupu 75 Ω bylo nastaveno externím voltmetrem naprázdno maximum 7 voltů. Schéma bylo nakresleno v simulačním programu EasyEda (představení na HW.cz). Jak je vidět z druhého zapojení, proud lze určit i nepřímo z úbytku na vnitřním odporu generátoru 75 Ω. Vnitřní odpor generátoru lze snadno zkontrolovat externím proměnným odporem a poklesem svorkového napěti na polovinu. Pro jistotu ale bylo zvoleno klasické měření proudu a napětí multimetry Metex s frekvenčním rozsahem 100 kHz.
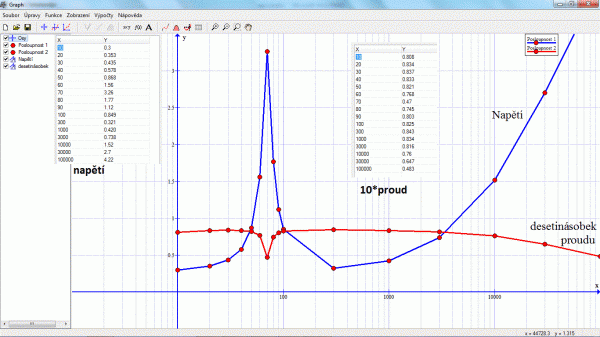
Obr. 8: Průběh napětí a proudu reproduktorem v závislosti na kmitočtu (program Graph)
Z průběhů je vidět, že proud se opravdu v závislosti na kmitočtu mění minimálně, takže pro určení rezonance opravdu stačí sledovat výchylku voltmetru. Pro přesnější určení rezonance by bylo vhodné podrobněji odměřit vrchol křivky. Větší chybou je ale absence hodnoty při kmitočtu 200 Hz. Měřeno bylo podrobněji v první dekádě kmitočtů s tím, že někde zde bude rezonance, zbytek charakteristiky byl změřen rychleji jen se dvěma hodnotami na dekádu.
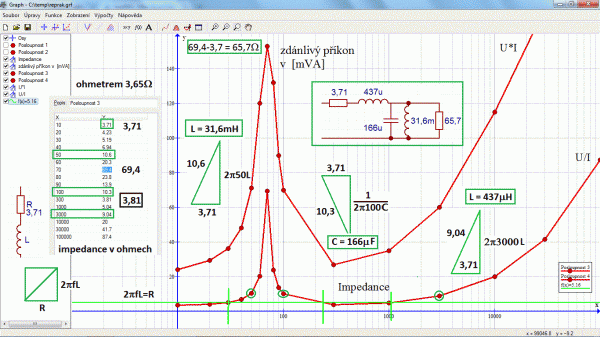
Obr. 9: Určení prvků náhradního modelu reproduktoru ze změřené impedanční křivky
Odpor kmitací cívky byl stejnosměrně zkontrolován multimetrem (3,65 Ω). Impedance reproduktoru je ale definována až jako nejmenší hodnota za rezonancí (3,81 Ω) a je vidět, že se hodnoty dle očekávání příliš neliší a jedná se tedy o čtyřohmový reproduktor. Zeleně je v grafu vyznačena konstanta 5,16 Ω, což je hodnota odporu cívky vynásobená odmocninou ze dvou (úhlopříčka čtverce fázorového diagramu). Pokud by se odečetly naznačené kmitočty, tak by z rovnice reaktance rovná se odpor (R = 2πfL a R = 1 / 2πfC) šlo určit prvky náhradního modelu reproduktoru v pořadí: indukčnost rezonančního obvodu, kondenzátor rezonančního obvodu a indukčnost kmitací cívky. Náhradní odpor tlumení rezonančního odporu se určí odečtením odporu cívky od rezonanční hodnoty impedance (65,7 Ω). Protože impedanční křivka je dost vodorovně a špatně se tedy určuje průsečík s konstantou 5,16 Ω a z logaritmické osy se kmitočet odečítá také obtížně, vezmeme nejbližší hodnoty z tabulky spočítaných impedancí (v obrázku vyznačeno tmavší zelení).
Při tomto složitějším řešení je ale zapotřebí k určení odvěsny fázorového diagramu použít Pythagorovu větu. Takže kdyby se úloha měla řešit častěji, bylo by vhodné vrátit se k původní myšlence určení mezního kmitočtu, kdy má fázorový diagram tvar čtverce. Tj. nastavit napětí naprázdno generátoru na maximum (7 V), zkontrolovat vnitřní odpor generátoru (dekádou nebo proměnným odporem a poklesem svorkového napětí na polovinu) a odměřit to jen voltmetrem po dosazení proudu z úbytku na vnitřním odporu generátoru (75 Ω). Po úpravě je modul impedance roven Z = 75U / (7-U), což odpovídá hodnotám určeným Ohmovou metodou. Pokud se podíváme do tabulky změřených napětí (obr. 8) je vidět, že napětí se mění v malém rozsahu, takže jmenovatel vztahu nemění příliš svoji velikost, takže opravdu stačí pro určení rezonance sledovat voltmetr (v čitateli je 75U). Z tohoto pohledu by na tom bylo ještě lépe buzení z měkčího výstupu generátoru Z = 600U / (7-U).
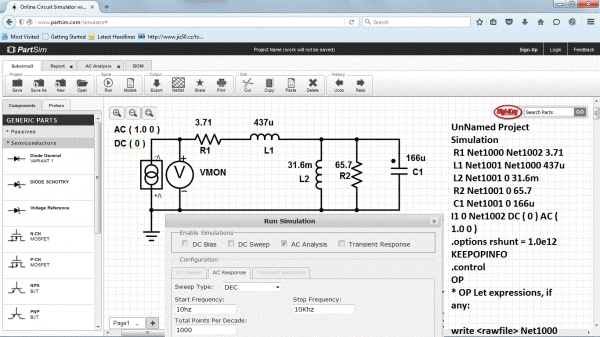
Obr. 10: Model reproduktoru zakreslený v on-line SPICE simulátoru PartSim
Takže jednodušší způsob určení parametrů by byl následující: odměřit lepším multimetrem odpor drátu cívky (3,65 Ω, tomu odpovídá napětí ze vzorce 325 mV), určit po kontrole generátoru odpovídající napětí ze vztahu Z = 75U / (7-U) pro 1,41násobný nárůst impedance při mezním kmitočtu (5,16 Ω, odpovídá napětí 451 mV) a pak pomalu ladit a hlídat nárůst a pokles napětí na tuto hodnotu a poznamenat si tři kmitočty. Z rovnosti odporu vinutí cívky a reaktancí pak určit parametry (3,65 = 2πfL a 3,65 = 1 / (2πfC)). Porovnáním obou napětí, jejichž poměr se blíží odmocnině ze dvou (451 / 325 = 1,39), je vidět, že by stačilo i hlídat 1,4násobný nárůst napětí oproti nejnižšímu kmitočtu.
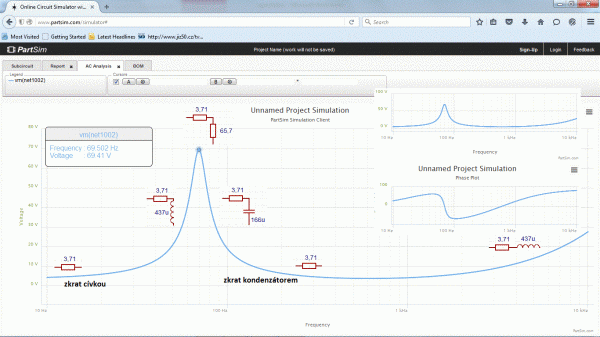
Obr. 11: Impedanční charakteristika reproduktoru odsimulovaná v simulátoru PartSim
K ověření správnosti modelu byl využit on-line SPICE simulátor PartSim a to z toho důvodu, že umožňuje při střídavé analýze .AC zvolit na svislé ose i napětí a nevnucuje decibely přenosu. Pro vykreslení impedance je využit Ohmův zákon a jako vstup se zvolí proud 1 A a pak je napětí na voltmetru číselně rovno ohmům. V pravém horním rohu je vidět, že program vykresluje i fázi. Zcela ve shodě s předpokladem, že při induktivním charakteru je kladná a při kapacitním záporná a při rezonanci je nulový fázový posuv. To by se také koneckonců dalo využít a určit rezonanci pomocí Lissajousových obrazců na osciloskopu.
Při simulaci byl zmenšen frekvenční rozsah o dekádu, protože u modelu stoupá v poslední dekádě impedance rychleji než u odměřených charakteristik a oblast rezonance by se nevykreslila pěkně. I to jde vysvětlit buď vlivem parazitních mezizávitových kapacit kmitací cívky, anebo omezeným frekvenčním rozsahem použitých multimetrů. Myslím si, že shoda chování elektrického modelu reproduktoru se skutečným reproduktorem je téměř dokonalá. Musíme mít ale na paměti, že to celé bude založeno na skutečnosti, že obvod lze řešit postupně pro různé kmitočty a zbytek lze zanedbat (obr. 11) a to nemusí být splněno pro všechny typy reproduktorů.
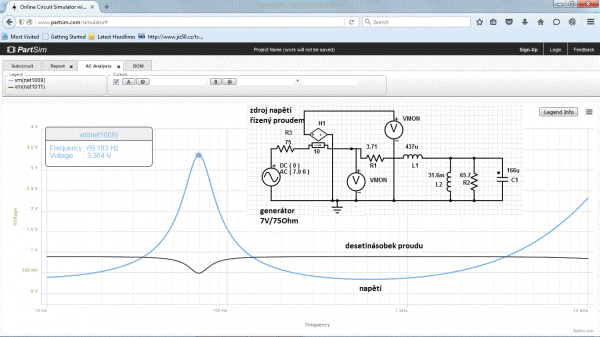
Obr. 12: Simulace provedeného měření napětí a proudu reproduktoru z generátoru 7 V / 75 Ω
Nejdříve se na reproduktor pohlíží jako na smotaný drát, který má odpor. Pak se začne uplatňovat reaktance virtuální cívky mechanického rezonančního obvodu. Nastane ideální rezonance paralelního rezonančního obvodu a zbyde jen sériové spojení jeho tlumení s odporem kmitačky. Nastává pokles impedance díky kapacitě rezonančního obvodu. Jeho reaktance se pak blíží téměř nule a impedance je tedy jen nepatrně větší než odpor drátu. Nakonec se uplatní reaktance kmitací cívky a celková impedance začne opět růst.
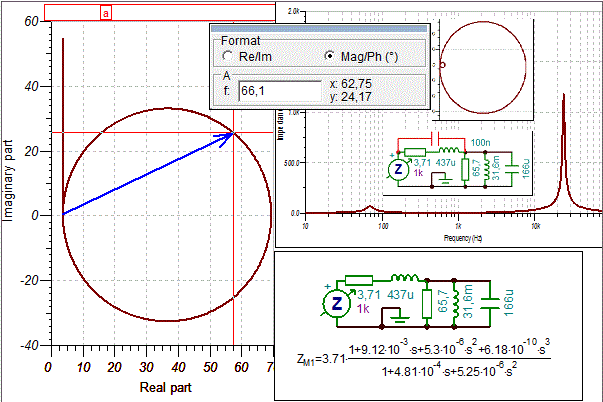
Na úplný závěr by přišly ke slovu mezizávitové kapacity kmitací cívky, došlo by k další rezonanci a „sešupu“ celkové impedance k nule, což je naznačeno na dalším obrázku vpravo (zvolena kapacita 100 nF). Program TinaPro umí zobrazit i komplexní Nyquistovu charakteristiku. V této charakteristice se lze snadno posouvat kurzorem. Zobrazuje se kmitočet s odpovídající velikostí a fází impedance. Alternativně lze zvolit i zobrazení reálné a imaginární složky impedance. V animovaném gifu je zvoleno zapojení bez parazitní kapacity kmitací cívky. Nejdříve to začne jako reálný odpor, ale nestoupá to kolmo nahoru jako u jednoduchého sériového spojení odporu s cívkou, protože to zakřivuje kapacita. Ve vodorovné ose (bez fázového posuvu) bude rezonance, pak se to zkratující kapacitou vrátí téměř na odpor drátu a pak to způsobně stoupá kolmo vzhůru jako sériové spojení odporu a indukčnosti kmitačky. Pokud se bude uvažovat i kapacita cívky (neměřeno), tak by se to zatočilo ještě jednou dokola. Pokud máte ostrou verzi programu anebo starou demoverzi TinaPro6, tak program umí spočitat i komplexní impedanci. Písmenko s zastupuje operátor j2πf (vztah bez parazitní kapacity 100 nF).
Obr. 13: Simulace modelu reproduktoru v komplexní rovině v programu TinaPro TI (volná verze) - pro animaci klikněte
Dovolím si položit provokativní otázku: Je rezonance reproduktoru prospěšná či nikoliv? Já si myslím, že bude spíše ku prospěchu věci. Jednak po zabudování reproduktoru do uzavřené ozvučnice - reprobedny se pravděpodobně zvýší tlumení a rezonance nebude tak výrazná. A dochází k ní na správném místě kmitočtové osy, tj. na počátku akustického pásma a tam už člověk zvláště při nižší hlasitosti slyší mizerně (viz křivky stejné hlasitosti). Takže zvýraznění sametových basů :-) je žádoucí. Navíc o něco podobného se konstruktéři reproduktorových soustav snaží záměrně v ozvučnici typu bassreflex. A tady je podobný efekt zadarmo. U výškového reproduktoru si s rezonancí, která bývá mnohem méně výrazná, není třeba dělat starosti. K žádnému hrbu nedojde, protože tomu zabrání reproduktorová výhybka typu horní propust, která rezonanční kmitočet na měnič vůbec nepustí.
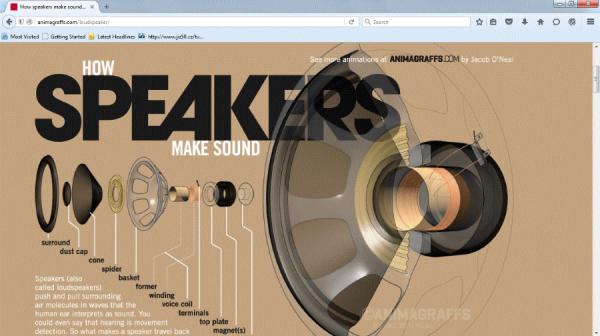
Obr. 14: Dokonalá animace reproduktoru na stránkách http://animagraffs.com/loudspeaker/
Na závěr bych ještě uvedl velmi pěknou animaci funkce dynamického reproduktoru od autora Jacob O´Neala. A na YouTube je také řada pěkných pokusů s No-Newtonian Fluid (asi kaše škrobu s vodou), např. zde.
Obr. 15: Měření výchylky membrány laserovým paprskem (den otevřených dveří VUT Brno)
Obr. 16: Měření akustického pole soustavou měřicích mikrofonů (den otevřených dveří VUT Brno)
Obr. 17: Profesionální umělá hlava (den otevřených dveří VUT Brno)
Obr. 18: Demonstrace funkce reproduktoru (neodymový magnet)